[Lecture] Descriptos: Computer Vision for Data Science
Parallelization
기존의 detector는 Gaussian의 1st derivative를 사용해서 peak(=local extrema) 것으로, scaling variant하다는 점이 결국 문제였다. 이를 해결하는 방법으로,
동일한 detector에 대해 (동일한 kernel size를 가지도록 고정), downsampling된 이미지들을 사용해서 detection을 다 해버리자!
Blob Detection
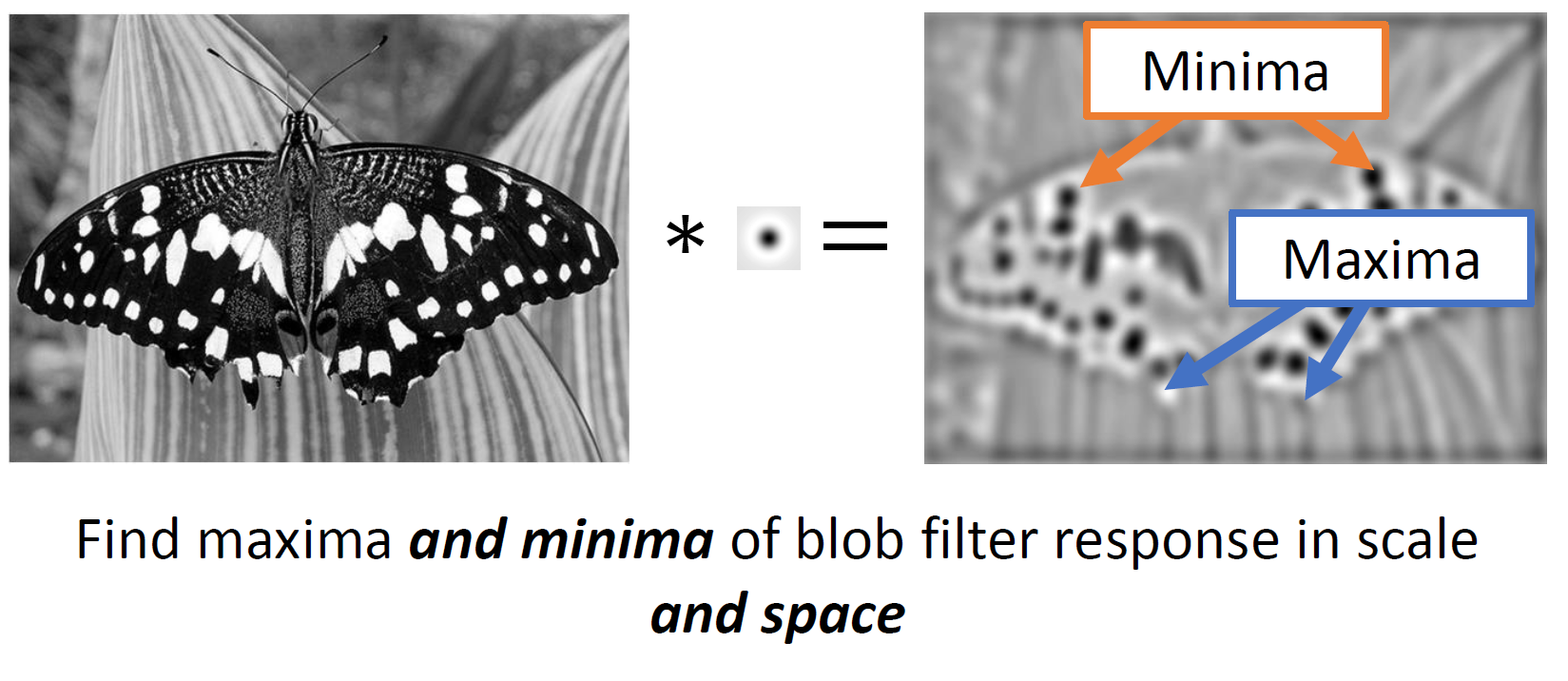
blob filter를 사용해서 minima와 maxima를 찾자!
Blob filter
Blob filter는 결국 Gaussian의 2nd derivative를 이용한다.
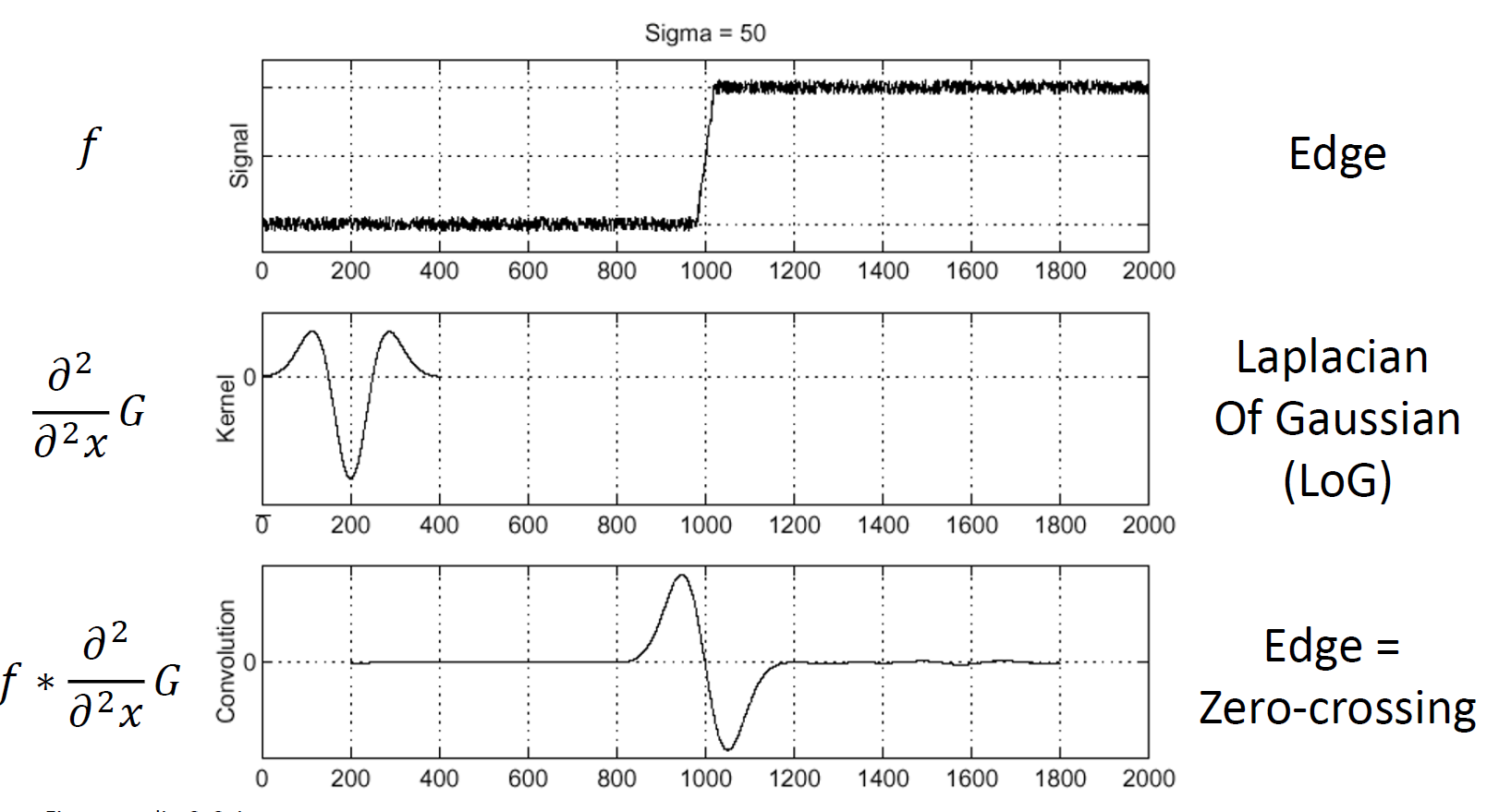
이렇게 각 axis에 대해 구한 2nd derivatives의 크기를 Laplacian of Gaussian이라고 하며 이를 이용한다!
그 결과 2nd derivative의 관점에선 zero-crossing을 찾는 것이 중요하다.
이를 laplacian의 관점에선 적절한 크기에 대해 peak(=extrema)를 찾는 문제가 된다!
Size
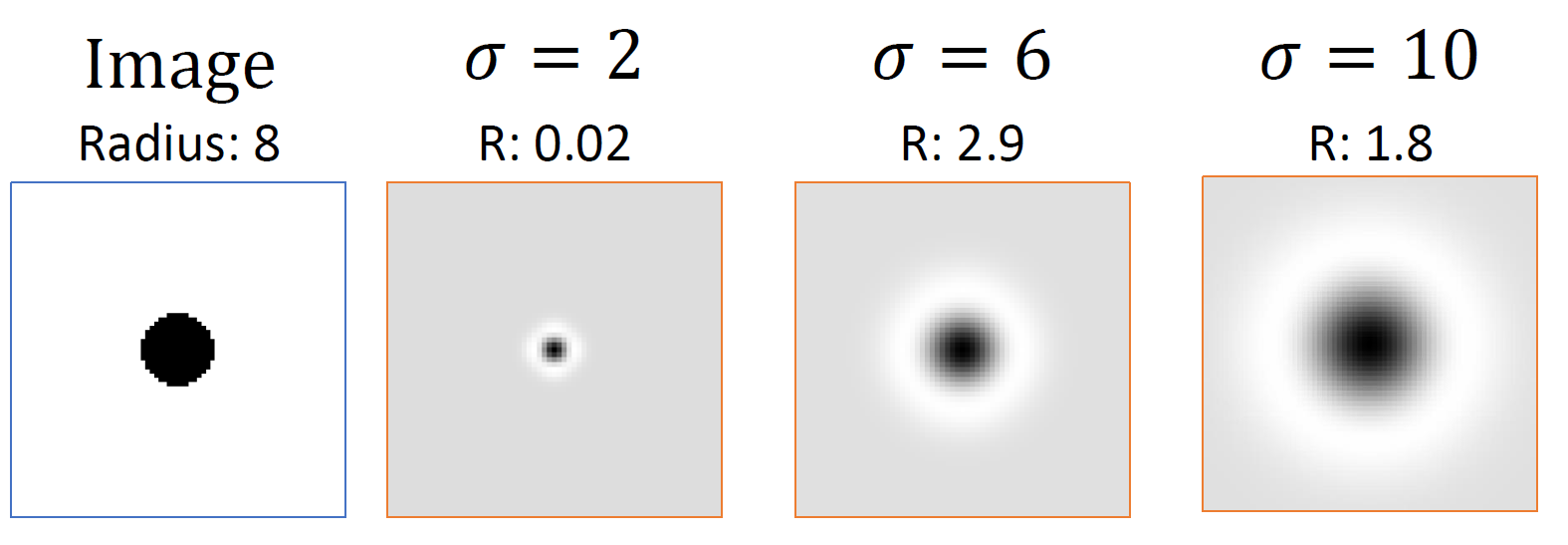
결국 laplacian을 잘 사용하기 위해선 적절한 크기의 Laplacian이 필요하고, 이를 조정하는 것이 결국 $\sigma$ 가 된다.
이와 연결하여 gaussian kernel에 대한 response에 시각적으로 보이는 일종의 크기, radius를 계산할 수 있게 되고, 관습적으로 $R=\sigma \sqrt{2}$ 다.
(이것의 의미로, 결국 적절한 scale을 정해주는 작업은 결국 $\sigma$ 에 의해 결정이 되니, 여러 scaline의 이미지를 사용해서 적용해보던 앞선 방법을 Blob filter에서는 여러 $\sigma$ 를 사용해보는 것으로 대체!)
Process
[1] Convolve image with scale-normalized Laplacian at several scales
여러 $\sigma$ 를 이용한 Laplaician 사용
즉 원래 Laplacian 값은 $\sigma$ 에 dependent했지만, 이를 곱한 값($=\sigma^2\nabla^2G$)를 사용하면서 normalized가 되는 것이고, 어떤 값으로 normalized를 하느냐에 따라서 response radius가 결정
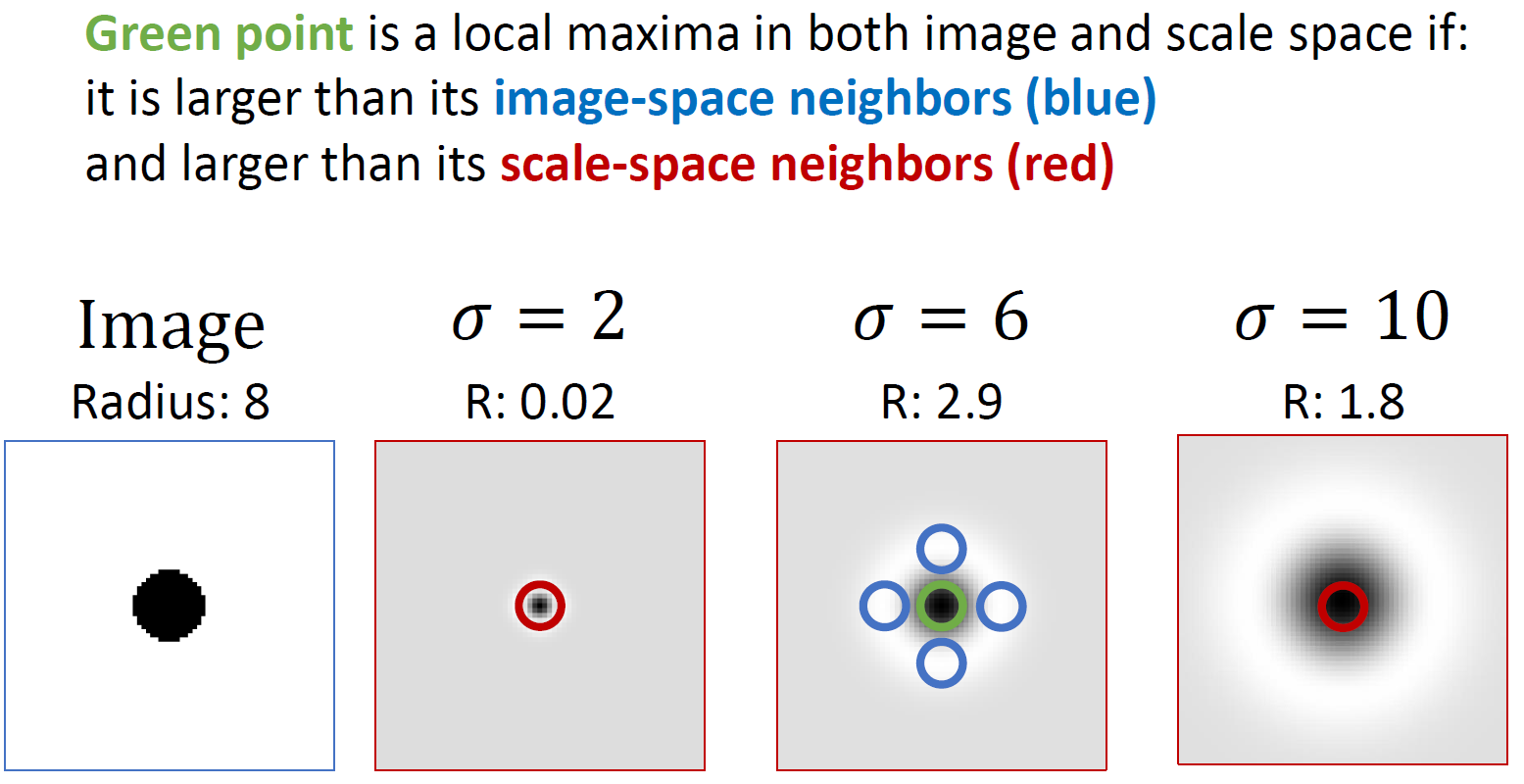
[2] Find local maxima and minima of nearby sqaure-shaped area in image $\times$ scale space
결국 각 scale(=$\sigma$)에 대해 local extrema를 계산해서 다 보이도록 하는 것
그럼 어떻게 extrema를 찾는가?
한 $\sigma$ 에 대해 search를 하게 된다면, 다른 sigma에 비해 Laplacian 값이 더 크면서(=scale space) 동시에 주변의 값보다도 더 큰 경우(image-space)
- 우리가 gray-scale image로 생각해보면 sigma에 대한 축을 만들게 되면 (H,W,sigma) 값이 생길 것인데, axis=2에 대해선 maximum이지만 axis=(0,1)에 대해선 minimum인 경우를 말하는 것같다.
Implementation
우리가 계속 2nd derivative인 Laplacian을 이용했다면, 이를 Difference of Gaussian(DoG)로 근사해서 사용할 수 있을 것!
(이는 Process step 1에서 Laplacian을 계산하는 것에 대한 구현인 것같다.)
이 근사의 특징은 2개의 gaussian의 차이(DoG)를 LoG의 근사로 사용한다는 것이고, 그러면 2개의 Gaussian은 결국 sigma 앞의 계수 $k$ 에 의해 결정되는 것이다.
즉 sigma가 서로 다른 gaussian 간의 차이값이 LoG 값으로 사용하는 것이고 이를 통해 한 scale에 대한 laplacian을 구하게 된 것.
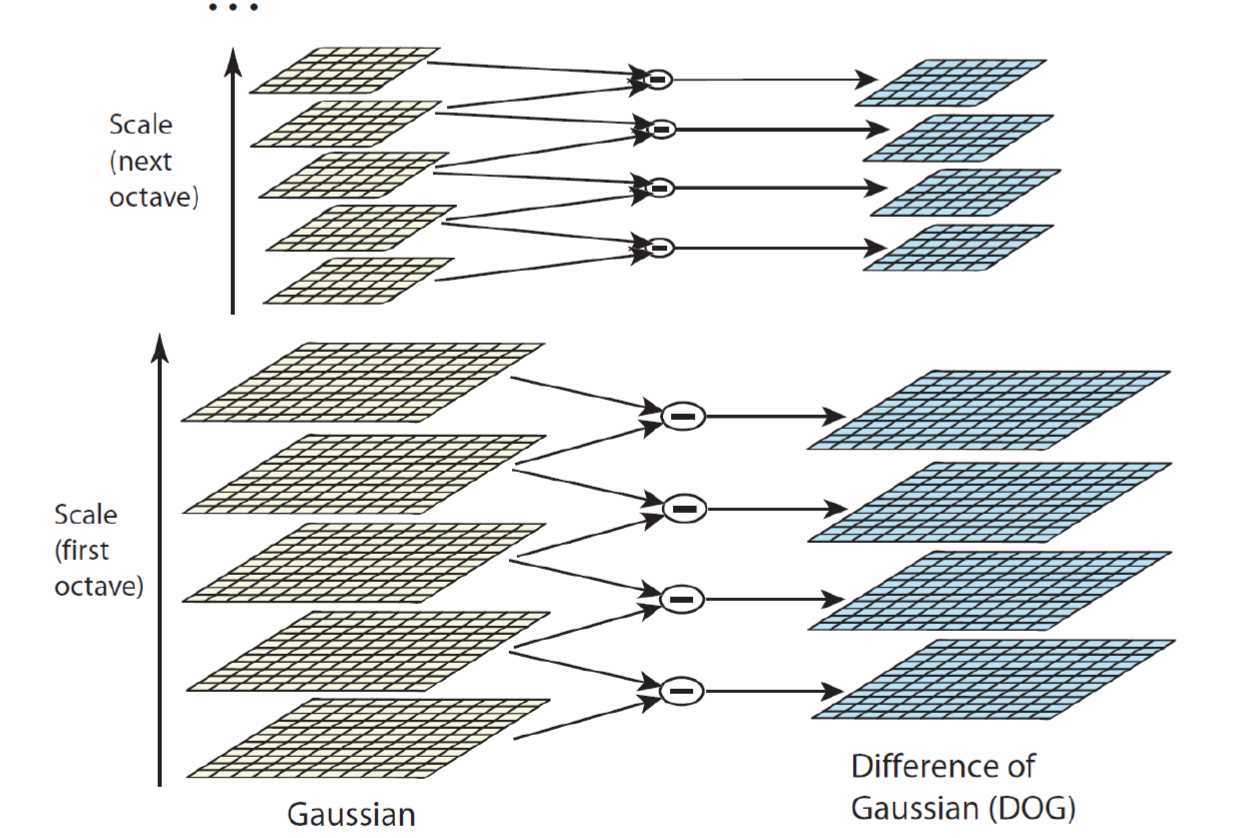
이를 여러 다른 scale에 대해 적용하기 위해서 우리는 downsampling한 이미지에 대해 동일한 gaussian filter를 사용하게 되면 굳이 scale 값을 바꿔가면서 laplacian을 사용할 필요가 없게 된다!
Describe it!
이전까지는 계속 corner나 edge, blob을 찾아낸 것에 해당하고, 이를 비교해서 matching하기 위해선 describe하는 과정이 필요!
즉 feature를 describe하기 위해서 고려할 것은
- scale
- rotation
- brightness
- ….
Scaling
앞서서 corner나 edge와 달리 scale에 무관히 feature를 찾는 방식으로 blob을 고안했고, 이렇게 찾은 각 blob들은 그에 상응하는 scale 값이 알려져 있다. 그래서 이 scale 값으로 원본 이미지를 rescaling하면 된다.
(즉 우리가 implementation과정에서 downsampling해서 blob들을 찾아냈고 그렇게 찾은 blob들 중에서 abs Laplacian이 가장 큰 녀셕이 blob이 되었으니, 그 가장 큰 녀셕의 downsampling scale factor를 이용해서 우리의 이미지를 rescaling한다는 것같다.)
Rotation
이미지의 rotation에는 어떤 feature도 다 invariant/equivariant 하지만, 서로 다른 방향성분들을 비교, align하기 위해선 이미지의 rotation을 측정할 필요가 있어서 등장한 것이 Historgram of Oriented Gradients(HOG)다!
그 중 SIFT라고 하는 알고리즘을 이용해서 이미지의 rotation을 측정한다.
이는 해당 여역에 대해 gradient의 방향성분 각 patch마다 계산하고, 이를 histogram으로 그려서 이 histogram을 feature로 사용하는 것!
- out-of-plane rotation rotation이 이미지 plane과 평행하지 않다면 동일한 대상이지만 놓치고 있는 target의 part가 존재할 것.
SIFT Process
- 관심 영역(=keypoints)을 계산
- 관심 영역에 대해서 16*16으로 scale 고정
- 한 image 내 4*4 patch로 나눠서 patch별 gradient의 8개의 orientation(결국 bin number 역할)의 histogram 계산(총 16개의 hisgtogram return)
- 16개의 patch마다 각 8개의 histogram bin이 생기니 총 128개의 feature 계산 완료!
- Properties
- gradient 기반이니 illumination에 무관하다(intensity translation은 무관)
- 한 이미지를 4*4 patch로 구성하니 shift나 rotation에 대해선 비교적 invariant하다
- 60도 정도의 out-of-plane에 대처 가능
- feature vector들 간의 distance metric이 유의미한 관계를 나타낸다(비슷한건 거리가 가까워짐)
- 다만 거리로 matching을 할때엔 threshold를 결정해야 한다.

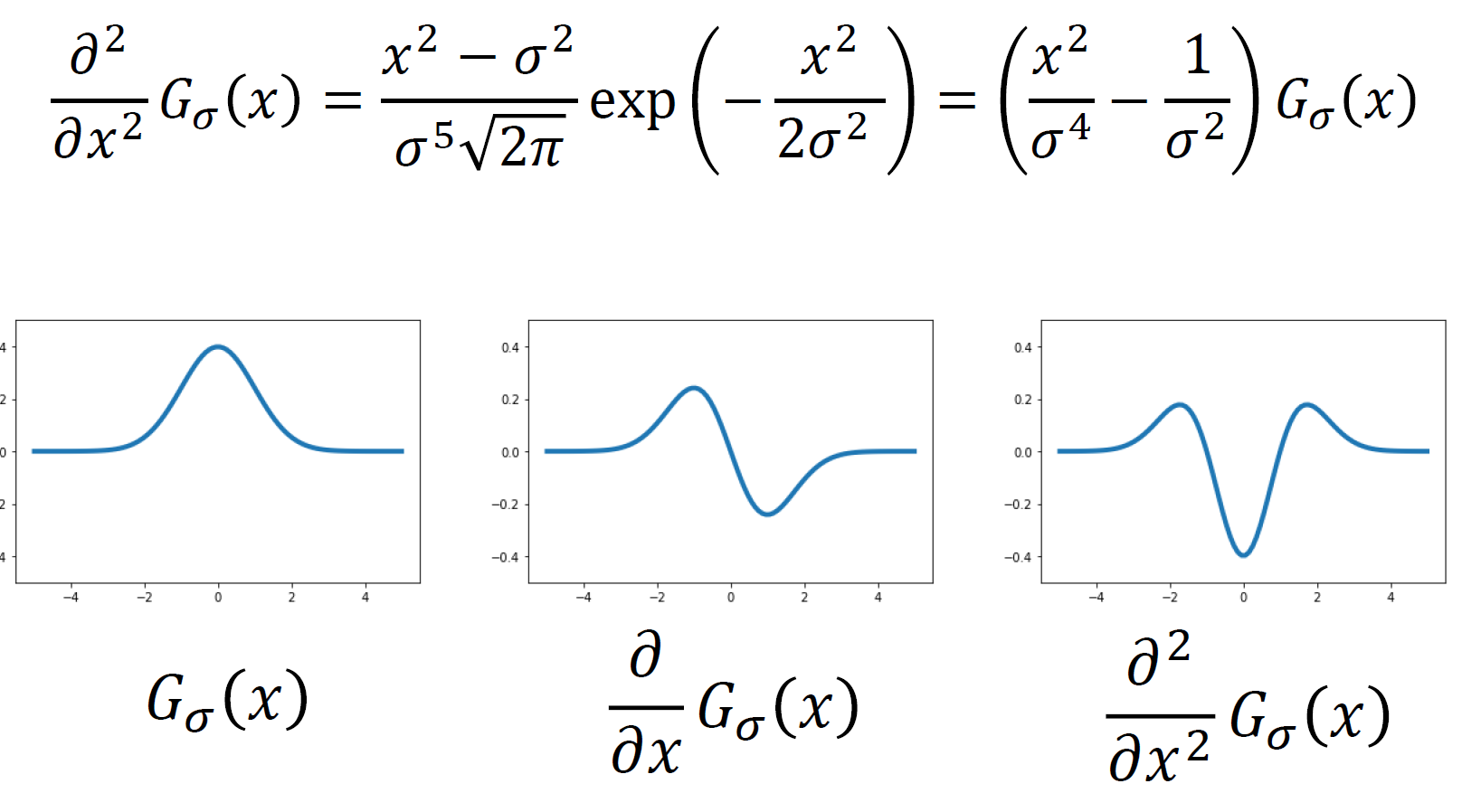


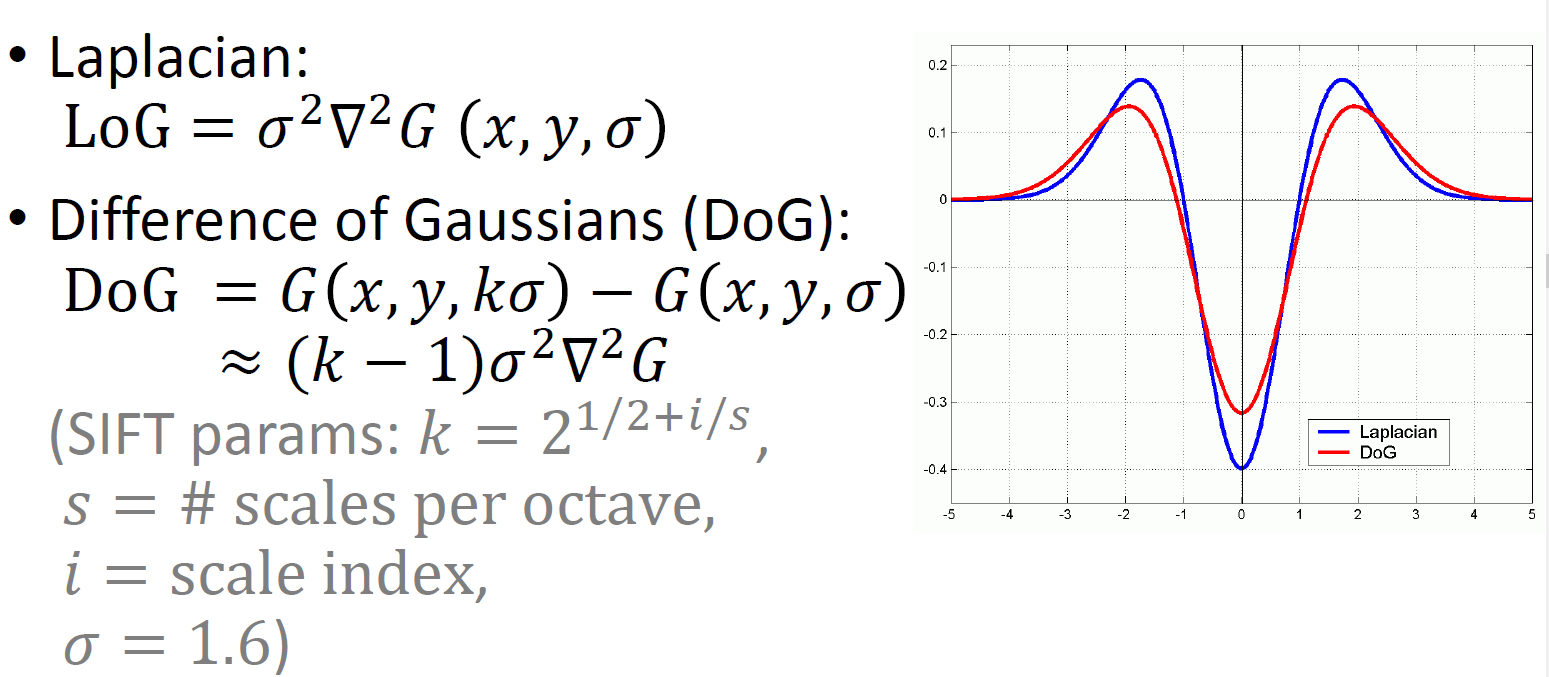
댓글남기기