[Lecture Summary] 02 Real Anaysis : Field
This contents is based on Lecture of 18.100A of MIT Open Course. Coverage will be Lecture from 4~. link
Overview
All we need to know once we learn about it is
- Useful inequality manipulation!
- inequality is relevent lubp!
Definition and Symbols
Field
- Two operations matter!
- Addition and multiplication
- Some properties should be satisfied
Ordered field
- ordered set $F$ with ordering $< s.t.$
- $\forall x,y,z\in F, x<y \Rightarrow x+z<y+z$
- $x>0 \mbox{ and } y>0 , \mbox{ then } xy>0$
$x+A$
- $\lbrace x+a \mid a\in A\rbrace$
$xA$
- $\lbrace xa \mid a\in A\rbrace$
Absolute value
- $\mid x\mid = x$ for $x\ge 0$ o.w. $-x$
Decimal representation(represent by digits)
- $x\in (0,1], d_{j} \in \lbrace 0,1,\cdots 9\rbrace$
- $x = \sup \lbrace 10^{-1}d_{-1}+10^{-2}d_{-2} + \cdots + 10^{-n}d_{-n} \mid n\in \mathbb{N}\rbrace$
Theorem
Let $F$ be an ordered field with the least uppber bound property. If $A \subset F$ is nonempty and bounded below, then $\inf A$ exist in $F$
Approach
- use $-A$ and find $\sup(-A)$ first
- LUBP is impactful!
- use definition of infimum and supremum.
- most of relation is based on the fact that it is ordered field.
There exists a unique ordered field, which is $\mathbb{R}$, satisfying that $\mathbb{Q} \subset \mathbb{R}$ and LUBP.
Approach
- Order property
- prove existence of supremum
- use the above theorem.
- Algebric property
- prove uniqueness of supremum
- uniqueness comes from equality
- use the fact that it is a field
(Archimedian Property, AP) If $x,y\in \mathbb{R}$ and $x>0$, then $\exists n\in \mathbb{N}$ s.t. nx>y
Assumption
- $x,y\in \mathbb{R}$
- $x>0$
- $x$ could be any positive value(even $\epsilon$!)
Want to show that
- $\exists n \in \mathbb{N} s.t. n>{y\over x}$
Approah
- Contradiction!
- $\mathbb{N}$ has lupb!
- find otehr value which is bigger than supremum
(Density of Q) If $x,y in \mathbb{R}$ and $x<y$ then $\exists r\in \mathbb{Q} s.t. x<r<y$
so to speak,
- rational numbers are dense in $\mathbb{R}$
- We can find another number which exists between for a pair of given real numbers.
Assumption
- $x,y \in \mathbb{R}$
- $x<y$
Want to show that
- $ny>nx+1$
- find $j\in \mathbb{N} s.t. nx<j, j\le nx+1$
Approach
- Split cases with respect to zero!
- we only solve the case of positive interval. Negative inteval case will be followed.
- AP does matter!
- Derive that $n(y-x)>1$
- Derive $S=\lbrace k\in \mathbb{N}:k>nx \rbrace$
- WOP for the smallest value.
$x = \sup S \iff x$ is upper bounded for $S$ and $\forall \epsilon >0, \exists y \in S s.t. x-e<y\le x$
This is important theorem!
Assumption
- $S \subset \mathbb{R}$
- $S$ is nonempty and bounded above.
$\sup(x+A)=s+\sup A, \sup(xA)=x\sup A$
Assumption
- $x\in\mathbb{R}$
- $A$ is bounded above
Approach
- Derive upper bound for $x+A$
- And then derive equality!
- Proof for existence of upper bound is not enough
- We need to prove that exact supremum of set. Use iff relation!
(Trianle Inequality) $\forall x,y \in \mathbb{R}, \left x+y\right \le \left x\right +\left y\right $
Approach
- Derive inequality so that we can use 5th property of absolute value!
Remark
- Reverse Triangle Inequality($\Delta-inequality$)
-
$\forall x,y \in \mathbb{R}, \left \left x\right - \left y\right \right \le \left x-y\right $
-
$\forall x \in (0,1], \exists \mbox{ unique digists } \lbrace d_j : i\in \mathbb{N} \rbrace s.t. x=0.d_{-1}d_{-2}\cdots \mbox{ and } 0.d_{-1}d_{-2} < x \le 0.d_{-1}d_{-2}+10^{-n}$
- for the first constraint, there could be several decimal representations
- to defince decimal representation uniquely, the second constraint does matter. Left hand-side strict inequality let the representation uniquely!
- Eg. ${1/over 2} = 0.4999\cdots$
- $0.50000\cdots$ does not satisfy the second constraint.
(Cantor) $(0,1]$ is uncountable
Approach
- Contradiction!
- Suppose that there exists bijection.
- maps from decimal representation to other values in that interval
- Function that flips a part of decimal representation
- Find out an element which does not map onto
- Suppose that there exists bijection.
- Use just the above theorem, which says that there are unique decimal representation
Want to show
- For arbitrary given (unique) real values, there does not exist decimal representations which uses natural number
Remark
- Even though $\mathbb{Q}$ is countable, $\mathbb{R}$ and $\mathbb{R} \setminus \mathbb{Q}$ is uncountable
- Proof of countablity is equivalent with derivation of bijection from $\mathbb{N}$ to a given set.
- Countability = Same cardinality = Bijection existence
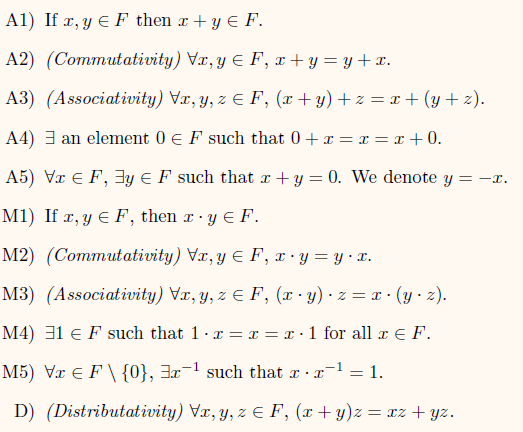
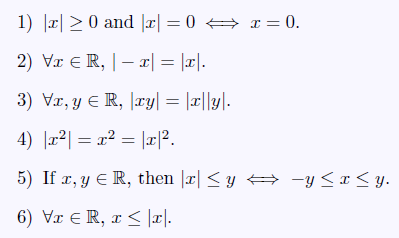
댓글남기기