[KMOOC 강화학습] Week 03-1 Shortest Path
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
동적계획법
- 최단경로 문제(shortest path problem)
- 외판원 문제(Traveling Salesman Probelm, TSP)
- 배낭문제(knapsack problem)
최단 경로 문제란?
시작점에서 종점까지 최단 경로를 찾는 것
Problem Formulation
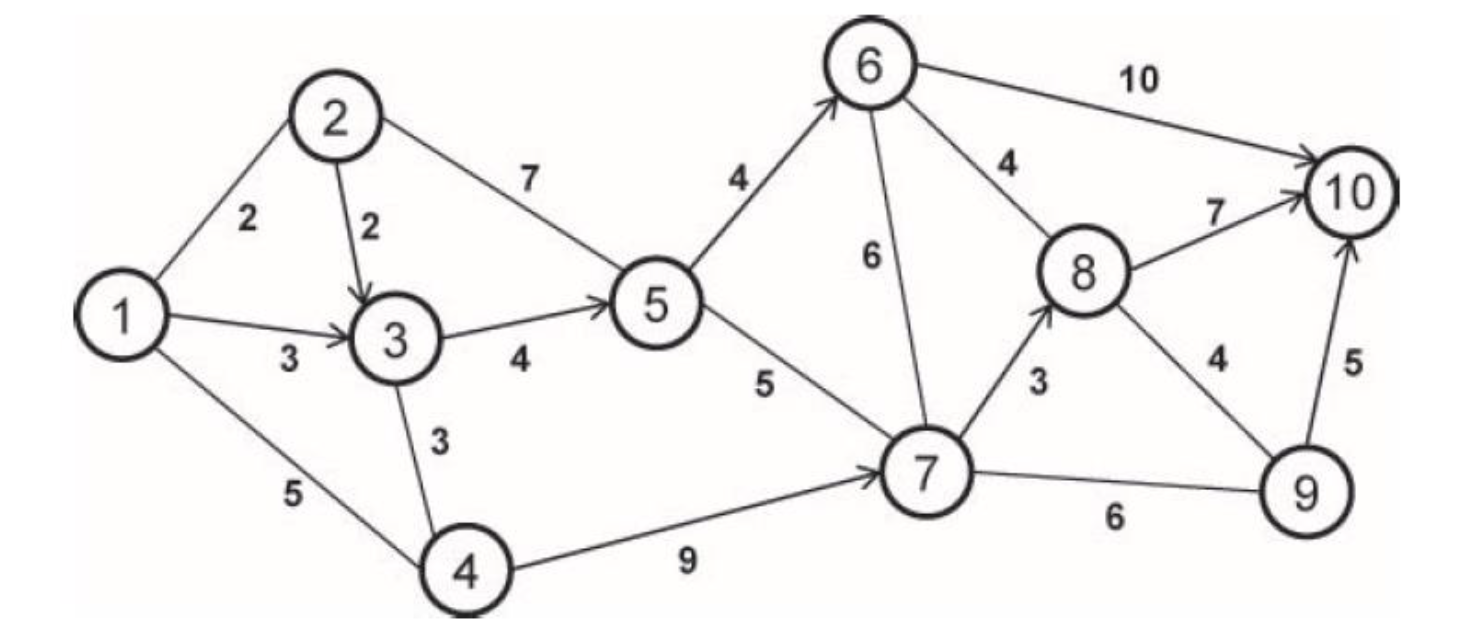
해당 문제를 node와 사이 연결된 arc가 있는 network라고 할 때, arc는 양방 통행이 가능하다고 생각하자.
그리고 node 간의 숫자는 걸리는 시간(비용)이라고 생각하자.
Solution
1) 모든 경우 나열
이건 풀기 어렵기 때문에 동적계획법으로 풀어보자!
동적 계획법의 관점
재귀식으로…?
- 상태와 행동을 정의
- 순차적으로 의사결경하는 방법으로, 한 node에 도착했을 때 다음 의사결정을 진행하는 방식으로 진행된다.
그렇기 때문에 현재 “상태”는 현재 “어떤 node”에 있는지를 말하게 된다. - 이 때 다음으로 이동할 node를 “선택”하는 것이 “행동”이다.
- 순차적으로 의사결경하는 방법으로, 한 node에 도착했을 때 다음 의사결정을 진행하는 방식으로 진행된다.
- 재귀식을 통해 가치함수를 결정한다.
- 최단 거리에 해당하는 거리나 시간($v((s_{t}))$)
- 비용은 $r(s_{t},s_{t+1})$ 로 나타낸다.
- 어떤 상태에서 종점까지 최종 소요 시간 $v(s_{t}) = \min_{s_{t+1}} [r(s_{t},s_{t+1}) + v(s_{t+1})] $
- 그런데 해당 재귀식으로 문제를 풀려면 하위 문제를 풀 수 있어야 가능하며 이런 경우, 순한 참조 문제가 생길 수 있다.
- 주어진 재귀식에서 순환 참조가 문제가 될 경우 결국 동적 계획법으로 문제를 풀 수 없을 것이다.
- 이런 경우, 추가적인 상태를 정의하고 그것을 이용해서 재귀식을 구현해야 문제를 풀 수 있게 된다.
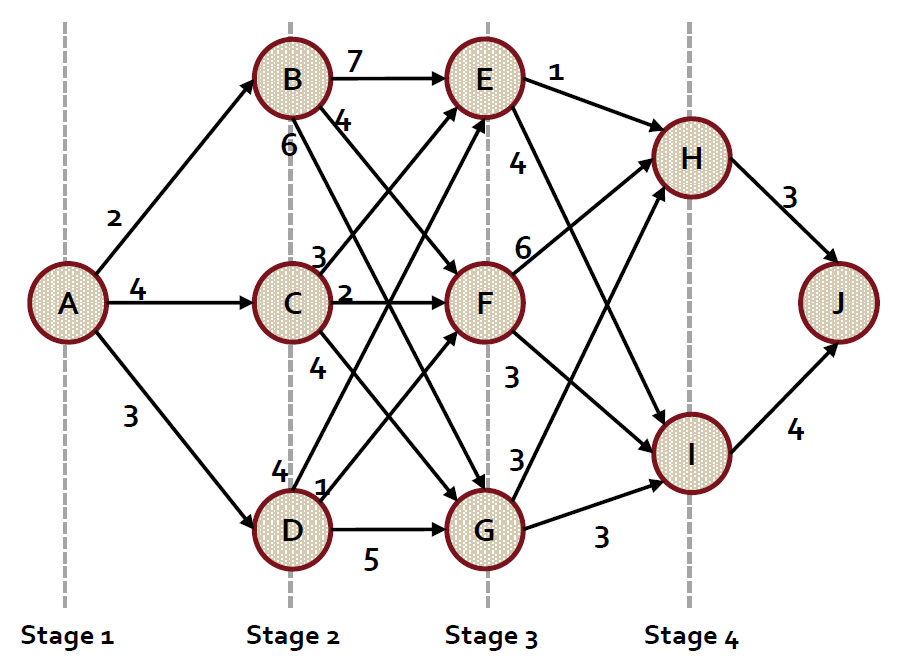
Stagecoach 문제
이런 문제가 생긴 건 서로 물고 물리는 관계, 즉 앞서 양방 통행이 가능하다고 했는데 그게 불가능하다고 헤보자!
이렇게 문제를 정의했을 때 가치 함수는 다음과 같다.
$v(s_{t}) = \min_{a_{t}} [ r_{t}(s_{t},a_{t}) + v(s_{t+1}) ]$
이 가치함수의 의미는 어떤 선택을 했을 때의 가치 혹은 비용을 말하므로 가령 B node에서 E node를 선택했을 때 E node를 선택함으로 생기는 비용과 E node에서 종점까지의 최소비용을 합쳐서 의사결정의 비용을 결정하게 된다.
이런 식으로 정의하게 되면 목적지에서 가장 가까운 곳부터 순차적으로 문제를 풀게 된다.
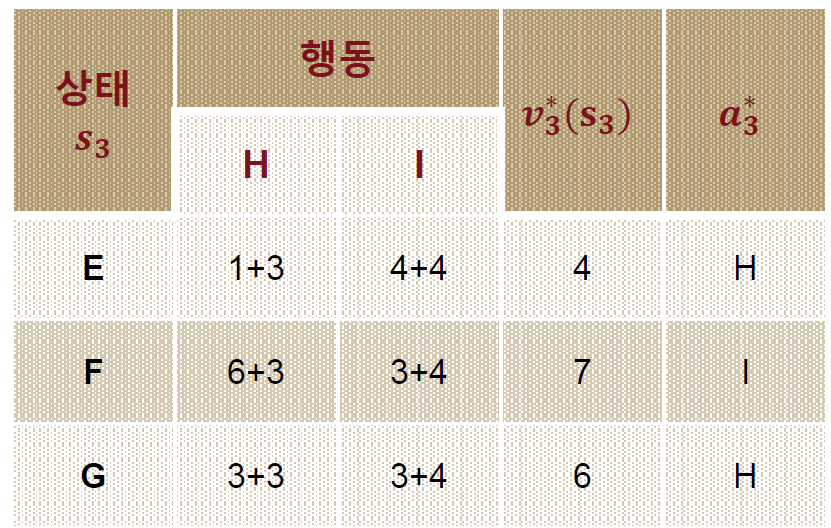
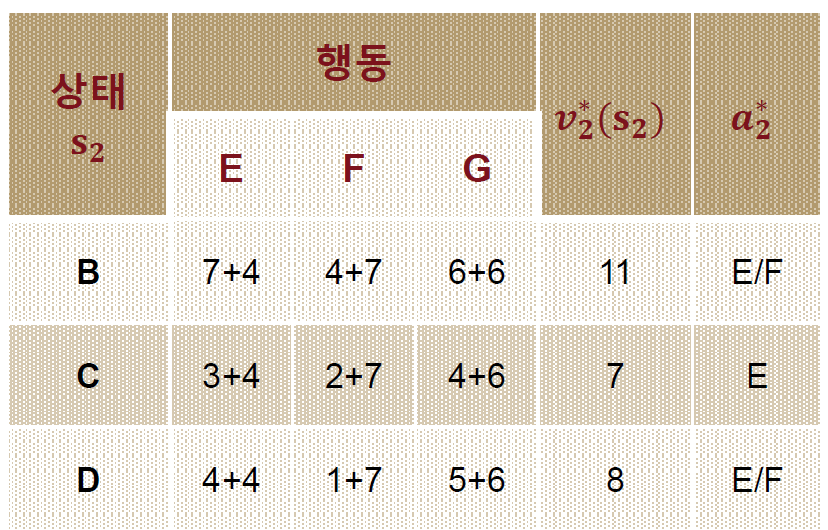
위의 사진에서도 볼 수 있듯이 어떤 상태(stage, $s$)에서 어떤 행동을 선택했을 때 최소비용이 $v_{s}$에 해당하고 그 때의 선택은 $a_{s}$이 된다!
위의 사진에서 중요한 것은 어떤 선택을 했는지보다 그 때의 최소 비용이 얼마인지가 중요하게 된다! E로 가든 F로 가든 결국 비용이 동일하면 구분하지 않게 되는 것이다.
이제 어떻게 하면 최소비용이 되는지 알고 싶다면, $a_{s}$ 의 기록을 추적하면서 정리하면 된다!
댓글남기기