[KMOOC 강화학습] Week 03-2 TSP
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
동적계획법
- 최단경로 문제(shortest path problem)
- 외판원 문제(Traveling Salesman Probelm, TSP)
- 배낭문제(knapsack problem)
외판원문제란?
여러개의 도시와 사이 거리를 알 때 가장 짧은 경로를 찾는 문제로, 물류 최적화 문제나 택배 배송 문제와도 연결되어 있다.
Problem Formulation
위의 식처럼 $(i,j)$ 간 비용을 나타내는 행렬로 표현할 수 있다.
- 상태: 이전에 어디 방문했고, 어디에 있는
- $N$ : 이전까지 방문했던 도시들의 집합
- $n$ : 현재 위치하는 도시
- 행동: 남은 도시중 어느 도시로 갈지 결정
- $n’ \in TOTAL- (N\cup set(n))$
- 가치함수: $N$의 도시를 다녔고, $n$에 있을 때 남은 도시를 다 방문하고 다시 원점으로 돌아가는데 걸리는 소요시간
- $V(N, n)= \min_{n’} [C(n,n’) + V(N\cup set(n), n’)] $
- 다음의 상태 : $V(N\cup set(n), n’)$
Solution
- 젤 마지막 상태의 가치함수는 0!
- 직전 상태 계산법
- ex. ({1,2,3}, 4) : 여기서 $n$은 4이며 남은 $n’$은 1이니 $C(n,n’)=6$
- $V(N\cup set(n), n’)=V({1,2,3,4}, \phi)=0$
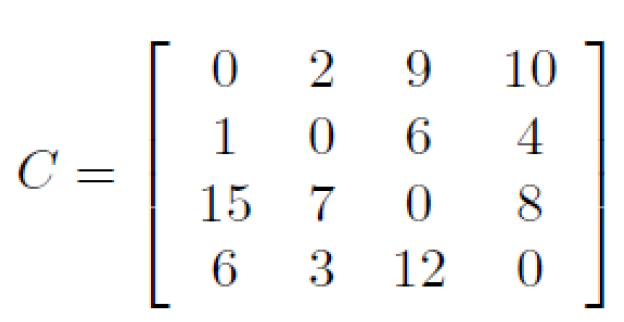
댓글남기기