[KMOOC 강화학습] Week 04-3 Markov Reward Process
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
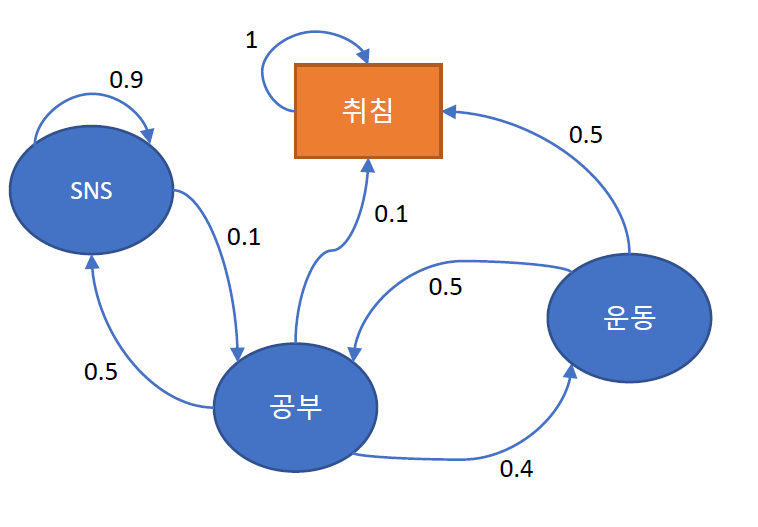
Markove Reward Chain
과거 선택과 무관히 현재 행동이 다음 행동을 결정한다고 할 때
- 상태 전이 확률로 표현가능하며
- 과거 이력과 무관히 현재 위치가 다음 위치를 결정하게 한다.
보상을 추가해보자
특정 상태에서 제공하는 인센티브로, 의사 선택은 확률적으로 결정되는데, 보상의 개념을 추가해보자
구성요소
- $S$ : 상태 집합
-
$P$ : 상태 전이 확률, $P[S_{t+1}=s’ S_{t}=s]$ -
$R$ : 보상함수 , $R_{s}=E[R_{t} S_{t}=s]$ - $\gamma$ : 감가율(discounting factor), 시간에 따라 보상의 가치가 변화한다.
- Episode : 특정 상태로부터 종료상태까지 (상태, 보상) sequence
- $G_{t}$ : 리턴, 감가율이 반영된 누적 보상, $G_{t} = \sum_{k=1} \gamma^{k}R_{t+k}$
markov chain이 주어져 있다면 위의 에피소드가 일어날 확률을 계산해볼 수 있고 각 에피소드별 리턴을 계산할 수 있다.
시작점의 영향
- 가치함수 : $v(s)$, 특정 상태에서의 리턴의 기댓값
- 이 때 특정 상태로부터 시작한 에피소드에 감가율이 고려된 보상의 총합이다.
즉 모든 에피소드를 나열 후 확률을 계산할 수 있다면 에피소드별 누적보상합을 계산할 수 있을 것이다. 그 결과 누적 보상을 계산할 수 있으니 기댓값을 구하게 되면 가치함수를 구할 수 있는 것이다!
프로세스가 진행됨에 있어 상태 $s$가 보상 측면에서 얼마나 좋은 상태인지 평가하기 위한 지표로 사용가능하다.
가치함수를 계산하려면
- 모든 에피소드 나열
- 모든 에피소드 확률 계산
- 누적 보상 계산
재귀식을 활용한 가치함수 계산
즉 어떤 상태에서 다음 단계로 부터 기인한 리턴과 현재 선택으로 인한 가치의 합으로 계산이 가능하다는 것이다!
여기서의 트릭은 reward는 고정이니 상태에 무관히 결정되어 상수로 나오고, 다음단계별 확률에 그 선택으로 인한 가치값들을 곱해서 계산가능하다.
해당 상태에서의 보상과 다음 상태에서의 가치들의 가중합을 고려한다.
위의 식에서 볼 수 있듯이 상태 전이 확률 행렬을 이용해서 나타낼 수 있다!
즉
$V=R + \gamma PV$
$IV=R + \gamma PV$
$(I-\gamma P)V=R $ 상태전이 행렬은 정방행렬로 항상 역행렬이 존재한다고 알려져 있다.
$V=(I-\gamma P)^{-1}R$
여기서 중요한 것은 보상과 에피소드의 개념이며
상태의 가치를 에피소드의 누적 보상합의 기댓값으로 산정하여 상태의 가치를 구한다는 것을 기억하자!

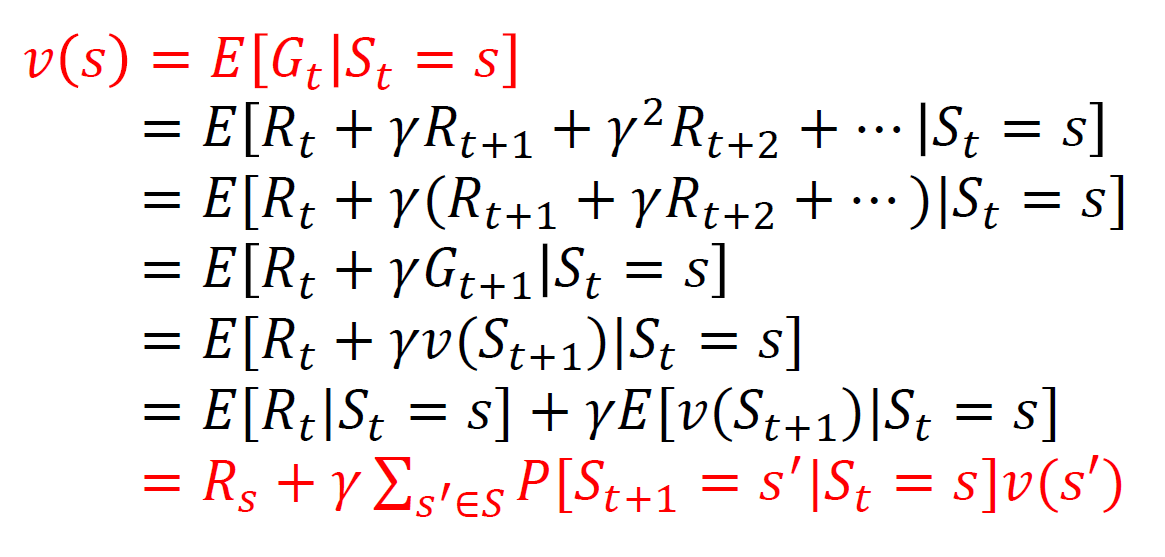
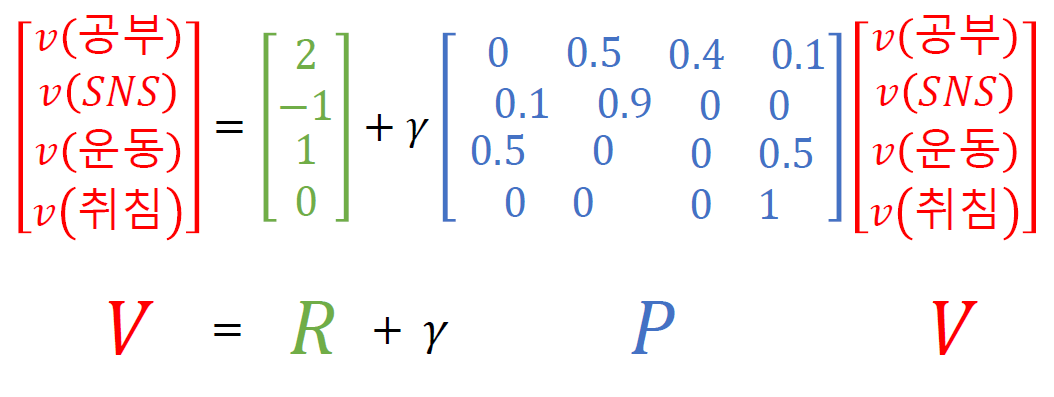
댓글남기기