[KMOOC 강화학습] Week 05-1 Markov Decision Process Overview
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
지금까지
- (확정적) 동적 계획법
- Markov Process
이 두 가지를 합친 것으로, 모델의 정의하기 위한 단계였다.
Deterministic DP 와 Stochastic DP의 차이점
- Deterministic : 특정 상태에서 액션에 따라 다음 상태가 정해져 있는 것.
- Stochastic : 어떤 상태에서 행동을 취했을 때 결과가 확률적으로 결정되는 것.
정의
확률적 동적 계획법의 Special Case로 강화학습의 수학적 기초에 해당한다!
- 단순히 확률 과정만을 다룬다고 할 때에는 의사결정을 고려하지 않음
- 전이확률에 따라서 다음 상태를 결정한 것이지 어떤 행동에 따라 시스템의 변화가 일어나지 않았었다.
- 하지만 순차적으로 의사결정한다는 점에서 의사결정자(Agent)가 확률 과정을 관찰하고 행동을 취함으로 인해 이후의 프로세스에 영향을 끼치게 된다.
결과적으로 Agent는 어떤 상태에서 선택한 행동에 따른 보상을 얻게 된다는 것이며
궁극적으로 관심있는 것은 평가 기준에 근거하여 각 단계별로 어떤 행동을 취해야 하는지 찾고자 한다.
구성요소
Time space
: 순차적 의사 결정 상황에서 의사결정 시점(decision epoch)의 집합으로
- 이산형이라면 단계(stage)의 집합
- T가 finite한지 infinite한지에 따라 finite-horizon / inifinite horizon MDP라고 불림
- 강화학습 알고리즘들은 infinite horizon MDP를 가정하고 지금은 finite한 경우 먼저 다룸
- finite한 경우 마지막 시점에선 의사결정이 없으며, 마지막 종료 시점의 보상(Terminal Reward)를 정의하게 된다.
State space
: 확률 과정 중 확률 변수들이 취하는 값들
- 의사결정을 할 때 필요한 최소한의 정보 혹은 환경에서 관찰이 가능한 최소한의 정보를 말함.
- 주로 이산형을 가정한다.
Action space A_S
- 상태에 의존적이라는 말은 어떤 상태에서 내가 취할 수 있는 상태가 달라진다는 것이며
- 어떤 상태 s일 때 가능한 Action의 집합을 말한다.
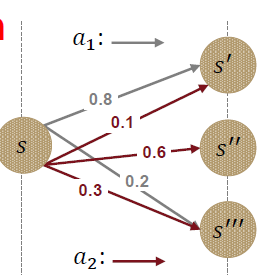
State Transition Probabilities P(s’|s,a)
- Deterministic과 stochastic 의 핵심 차이
- 현재 상태 s에서 어떤 행동 a를 취했을 때 다음 의사 결정 시점에서의 상태 s’를 결정하게되는 확률
- 선택에 따라 나오는 결과의 확률이 다 달라지는 것
보상 r_t(s,a)
의사결정 t에서 상태가 s일 때 행동을 a를 취하는 경우, 환경으로 부터 얻게되는 보상의 기댓값으로 상태와 행동에 의존한다.
- 상태 전이 확률과 보상함수로 서술하는 경우
$r_{t}(s,a) = \sum_{s’} p_{t}(s’\mid s, a) r_{t}(s, a, s’)$
- finite horizon MDP의 경우
$r_{N}(s)$ : 마지막 단계가 N일 때 의사결정이 없지만 그 단계에서 얻게되는 보상(terminal reward)
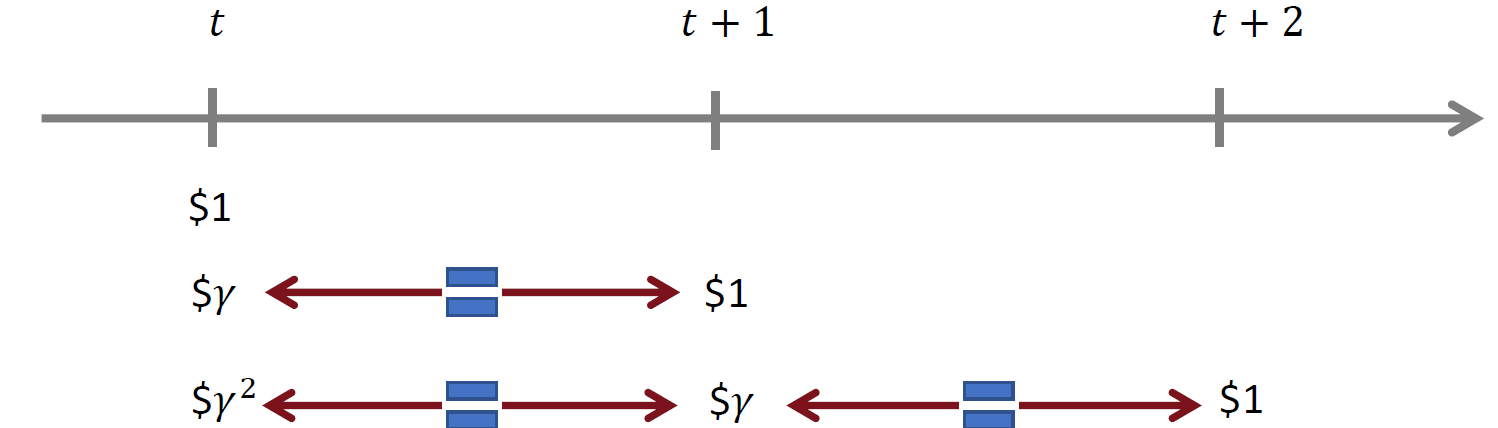
감가율(discount factor)
현재 받을 수 있는 보상은 미래에 받는 보상보다 가치가 높다는 것으로, 현재의 보상의 가치가 더 높음을 암시한다!
그렇기 때문에 미래에 받게될 보상에 대한 불확실성을 고려한 신뢰도를 말한다.
즉, 미래의 보상을 현재 가치로 환산할 때 얼마나 될지 알려준다.
MDP Policy
의사결정규칙(Decision Rule)
어떤 의사 결정 시점 t에서 시스템에 상태 s가 주어졌을 때 어떤 행동을 취해야 하는지 알려주는 함수
- 분류
| Deterministic | Probabilistic | |
|---|---|---|
| History-Dependent | HD | HP |
| Markovian | MD | MP |
- History-dependent : 과거의 모든 이력을 입력으로 받아 다음 행동을 결정하는 방식
- Markovian : 현재 상태만 고려해서 행동를 결정
MD의 경우 $\delta_{t}(s)$ 로 표현되고 MP의 경우 $\delta_{t}(a\mid s)$ 로 표현된다.
강화학습 메커니즘 설계에서는 확률로 서술한 MP가 유리하다.
Policy
- 매 단계별 의사결정 규칙들의 집합
- 모든 시점에서 동일한 정책이 적용된다면 stationary하다고 한다!
참고로 infinite horizon MDP에서는 모든 시점에 의사결정 정책이 동일한 stationary policy($\pi=\delta^{\infty}, \delta(s)=\pi(s)$)에 관심이 있다.
댓글남기기