[KMOOC 강화학습] Week 05-2 Markov Decision Process Example
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
주사위 던지기 게임
규칙
- 매 라운드 go 와 stop 가능
- stop하면 8달러를 받고 끝난다.
- go를 하면 4달러를 받고 주사위를 던진다
- 주사위가 1 혹은 2가 나오면 종료가 되며 그렇지 않으면 다음 라운드로 진행된다.
MDP Formulation
시간공간
매 라운드가 의사결정 집합으로 $T=[1,2,3,…]$
상태 공간
게임을 진행하거나 종료하거나 2가지 상태에 있다.
$T=[in, end]$
Action space A_s
Action space는 상태에 의존하기 때문에 각 상태애 따라 행동이 달라지게 된다.
게임 중이라면 다음라운드 할지 말지 결정하는 시점에서 행동은 go 와 stop이며 게임이 끝난 상태라면 stop뿐이다.
$A_{in}=[go, stop]$
$A_{end}=[stop]$
상태 전이 확률
이전의 이력은 상관이 없다. 현재 어느 상태인지가 중요하기 때문에 Markovian Property를 만족한다!
중요한 것은 상태 전이 확률은 현재 상태s와 행동 a가 주어졌을 때의 다음 상태 s’에 대한 확률이기 때문에 모든 경우의 값이 나와야 한다!
$P_{t}(in\mid in,go)=2/3$
$P_{t}(end\mid in,go)=1/3$
$P_{t}(in\mid in,stop)=0$
$P_{t}(in\mid in,stop)=1$
$P_{t}(in\mid end,stop)=0$
$P_{t}(end\mid end,stop)=1$
보상
어떤 상태에서 어떤 행동을 취함에 따른 보상의 기댓값이다.
$r_{t}(in,stop)=8$
$r_{t}(in,go)=4$
$r_{t}(end,stop)=0$
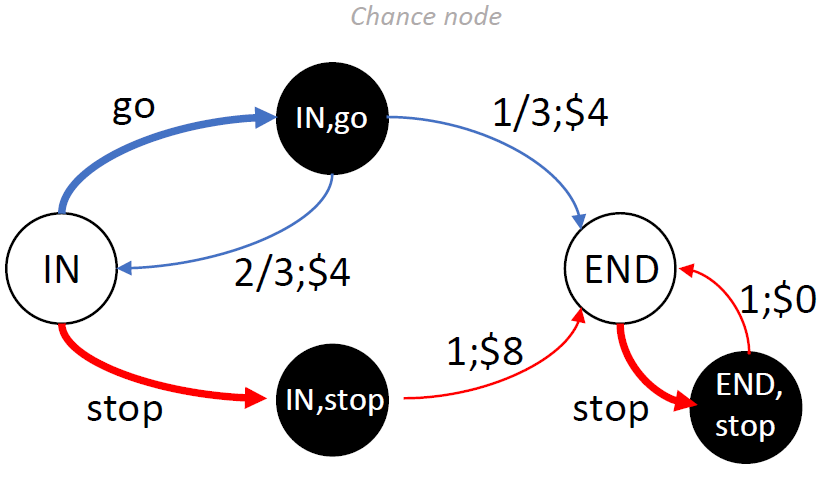
전체 구조도(chance node)
재고관리 예시
규칙
- 매달 시작 시점에 주문
- 수요는 한달간 발생하고 배달이 마지막에 진행한다.
- 만약 누적된 수요가 재고보다 높으면 품절처리하며
- 월간 수요 분포는 달라지지 않고, 비용도 고정
- 물류센터에는 최대 M개의 물품만 보관 가능
notation
$s_{t}$ : t번째 달 시작시점에서의 재고 수준
$a_{t}$ : t번째 달 시작 시점에서의 주문량
$D_{t}$ : t번째 달의 수요
$p_{j}$ : 수요가 j일 확률
$F(u)$ : 재고 수준이 u일 때 기대 수익
$o(u)$ : 주문량이 u일 때 주문 및 구매 비용
$h(u)$ : 재고수준이 u일 때 한달동안의 재고 보유 비용
MDP Formulation
시간공간
매달에 해당
$T=[1,2,3,…]$
상태 공간
주문 전에 보유하고 있는 재고 수준
$T=[0,1,…M]$
행동 공간
발주전 재고 수준 및 창고 용량을 고려한 주문량으로 최대 M-보유량 만큼 가능하다.
$A_{s}=[0,1,2,…,M-s]$
상태전이확률
기억할 점은 모든 상태, 모든 행동에 대해서 다음 상태를 다 정의해야 한다!
- 현재 재고 상태가 s개 이고 a개를 발주했다고 하자
- 다음시점에서의 상태는 s+a개를 가지고 장사하고 남은 재고 수준을 말한다!
- 그렇기 때문에 s+a개보다 더 많이 재고를 가질 수 없어서 확률은 0
- 그리고 다음 상태가 j일 확률은 s+a-j개 만큼 판 것!
- 재고가 0일 확률은 수요가 s+a이상 발생한 것으로 수요(D)가 s+a이상 발생한 것이다.
보상
이익 = 수익 - 비용
$r_{t}(s,a)=F(s+a)-O(a)-h(s+a)$
정책
매 단계별로 어떤 상태를 취해야하는지 결정하는 함수로,
위의 경우에는 (s,S)에 대해서 결정되는 것이다.
(1,10)의 경우에 u가 2라면 주문하지 않게 된다. 0이라면 10-0=10개를 주문하게 된다.
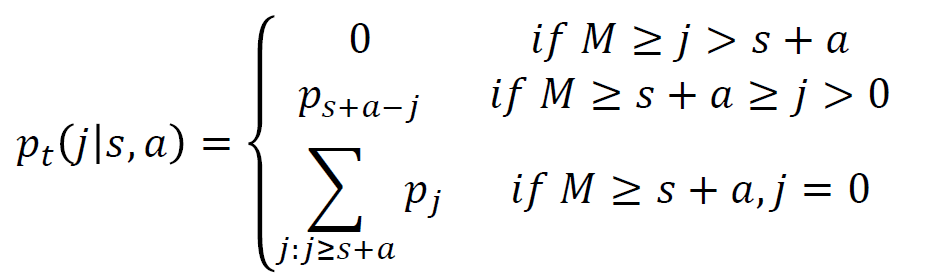
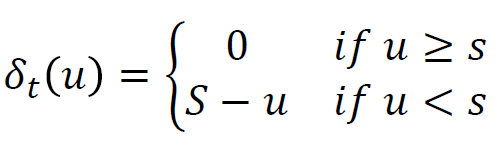
댓글남기기