[Lecture Summary] 15 Algorithm and Data Structure : DP Subproblems

This contents is based on Lecture of link

Overview

KEY idea of DP is

• subproblems have dependencies which overlap for several times. We can formulate that dependencies into DAG.
• Solve problem with Top-down approach which re-use already solved and recorded solutions. Recurse!
  • Iterating subproblems can be considered as Bottom-up approach. Careful “Brute Force”!

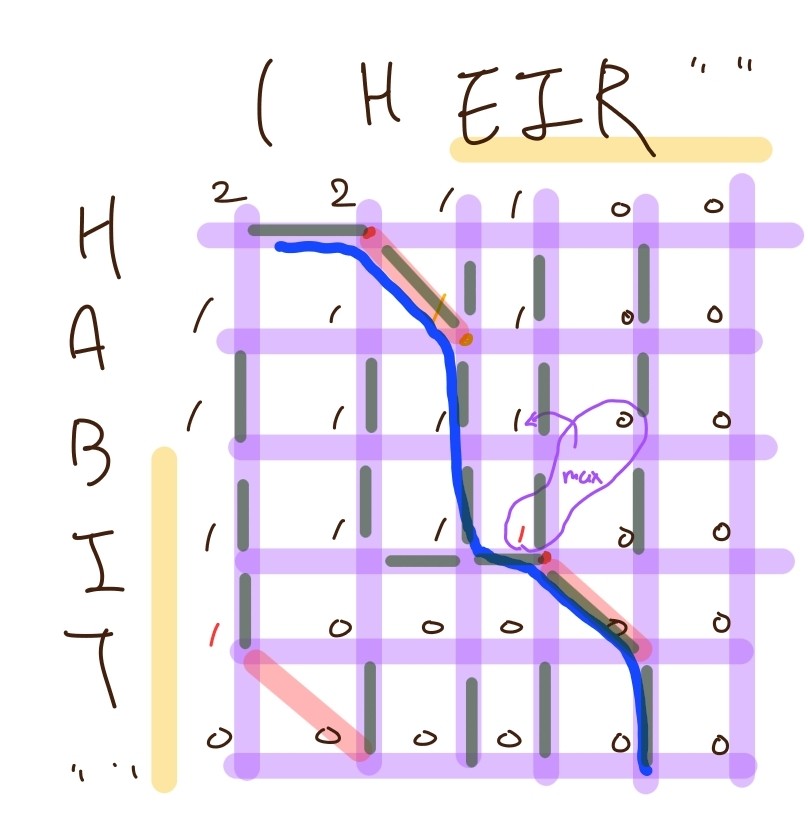
Longest Common Subsequence(LCS)

• Input: two strings $A$ and $B$
• Output : longest subsequence of $A$ that is also a subsequence of $B$

Something different from “Bowling” problem is that LCS requires 2 inputs and therefore subprblems for multiple inputs. To do so, multiply(cross product) subproblem spaces!

Formulation

• Subproblems :
  $L(i, j) = LCS(A[i:], B[j:]), i\in [0, \mid A \mid ] j\in [0, \mid B \mid]$

• Relation :
  $ L(i,j) = $
  (if $A[i]==B[j]$), $1 + L(i+1, j+1)$
  (else) $\max \lbrace L(i+1, j), L(i,j+1)\rbrace$
  

• Topological Order :
  (Decreasing index order)
  for $\mid A \mid \cdots 0$ for $\mid B \mid \cdots 0$

• Base Case :
  $L(i,\mid B \mid) = L(\mid A \mid, j) = 0$

• Original Problem :
  $L(0,0)$

• Time :
  

Category	Time
# of subproblems	$(\mid B \mid+1)(\mid A \mid +1)$
nonrecursive work	$O(1)$
In total	$O(\mid A \mid\cdot \mid B \mid)$

We can think of this solution as follows:

• For a given state(position) $i$ and $j$, check whether they are same with each other
• If they are different, then drop it!
• Check the matches only and count left-over.

Example

Longest Increasing Subsequence(LIS)

• Input: one strings $A$
• Output : longest subsequence of $A$ that strictly increase
  • String is int

The thing is that we need an information to determine wheter LIS includes current string or not.

Formulation

• Subproblems :

$L(i) = LIS(A[i:])$ that starts with $A[i]$. This constraint does matter to solve this problem. Because we do not know whether $A[i]$ is included in LIS or not, we assume that it does.

• Relation :

Naive approach : $ L(i) = \max \lbrace L(i+1), 1+L(i+1) \rbrace$ does not work because it does not support the above constraint.

Final approach : $L(i) = 1 + \max \lbrace L(j) \mid i < j \ge n, A[i] <A[j] \rbrace \cup \lbrace 0 \rbrace$
✔️ The first term originated from the constraint that $A[i]$ is included in LIS
✔️ Union is devised to support case that $A[i]$ always larger than following String.

• Topological Order :

Decreasing $i$

• Base Case :

$L(\mid A \mid) = 0$

• Original Problem :

$\max \lbrace L(i) \mid i \in [0, \mid A\mid] \rbrace$.
We can consider this solution as if we assume the starting point of LIS, then we can define LIS value and search every case of LIS

• Time :

Category	Time
# of subproblems	$(\mid A \mid)$
nonrecursive work	$O(\mid A \mid)$
In total	$O(\mid A \mid\cdot \mid B \mid)$

Time to run non-recursive work is the number of cases of starting LIS. We can improve time using AVL tree augmentation!(TODO)