[Lecture] Cameras: Computer Vision for Data Science
Projection
Pin-hole Model
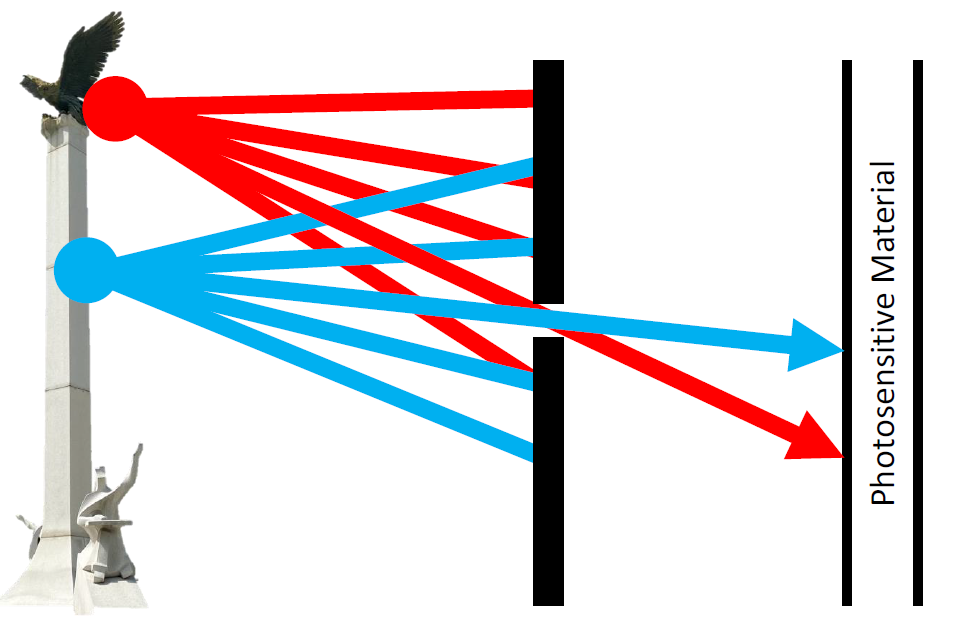
사람들이 사진을 이해할 땐 결국 Pin-hole 모델로 이해한다!
이는 빛이 여러방향으로 오지만 결국 하나의 작은 구멍을 지나서 상이 맺힌다고 이해하고 그렇기 때문에 상이 뒤집혀지는 것
Modelling
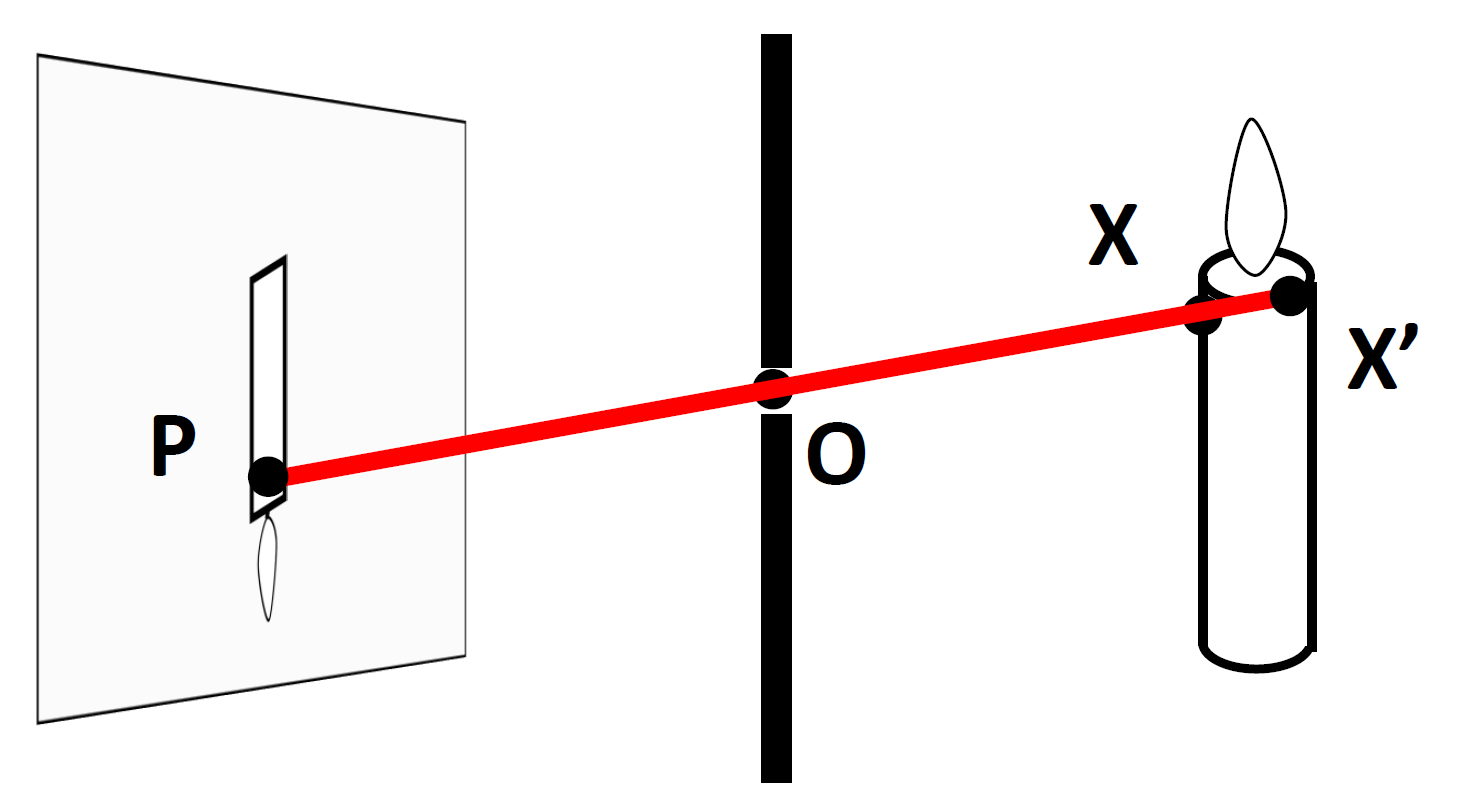
그렇기 때문에 결구 물체(target)의 상(image)는 일종의 3D 공간의 Projection에 해당하는 것으로 보게 된다. 그렇기 때문에 같은 점에 projection 되기도 하며, 맺히지 않는 곳도 존재할 것!
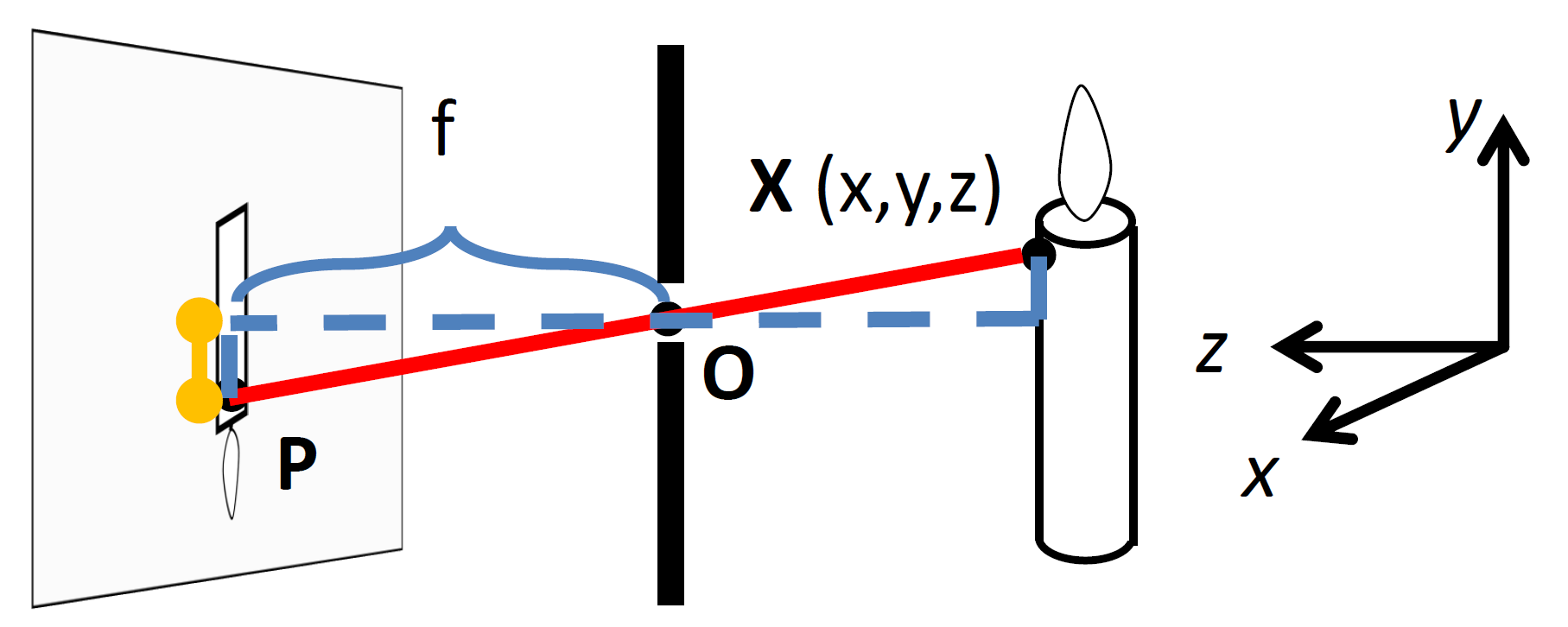
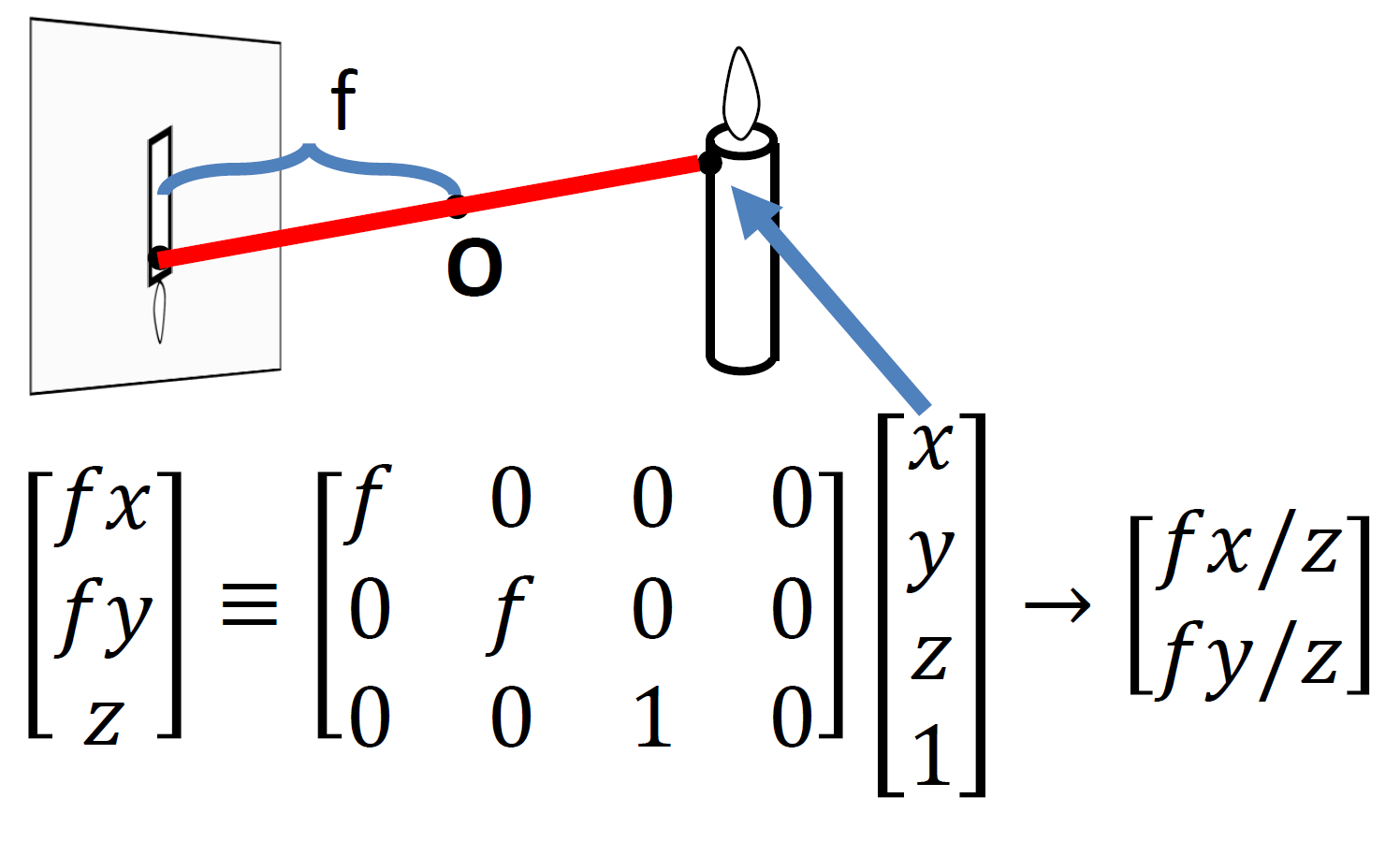
이를 모델링하자면, 3D 공간상 좌표$(x,y,z)$를 focal length $f$를 이용하면 $(fx/z, fy/z)$로 정의할 수 있다.
Properties
- Vanishing Point(VP)
결국 3D에서 projection을 하게 된다면 하나의 점으로 수렴하게 되고, 이 점이 바로 소실점(vanishing point)이다
이 때 3D에서 평행한 점들만 VP로 모이게 됩니다! 즉 아무런 선들을 image에서 확인했을 때 소실점으로 수렴하는 것은 아닙니다.
- Perspective
우리가 어떻게 바라보느냐에 따라서 projection도 달라진다. projection이 달라진다면 결국 2D 좌표도 달라진다는 것인데, image가 맺히는 시스템(예. 카메라)가 고정인 상태에서는 결국 $(fx/z, fy/z)$를 보면 z에 따라서 결정이된다. 이 $z$가 항상 동일한 경우를 fronto-parallel하다고 하며 이 때 scaling은 $f/z$만큼 되고 그 외의 값들은 conserved된다.
Equation
- Original
$(x,y,z) \to (fx/z, fy/z)$
이러한 변환식은 non-linear하며, z가 0인 경우에는 undefined!
- Homogeneous Coordinates(HC) : $(u,v,w)$
일종의 z를 1로 생각한다! 즉, focal depth를 1로 고정해놓고 생각한다는 것.
$(u,v,w) \to (u/w, v/w, 1)$
이 때 HC는 triple equivalent한 관계를 가지게 되는데 이러한 equilvalent는 평행한 경우를 말한다.
Formulation
결국 우리가 하려고 하는 것은 3D 객체를 2D상에 표현하는 것이고, 2D상에 표현한다는 것은 결국 선으로 객체를 표현한다는 것!
그렇다면 선은 어떻게 정의될까?
이는 기존에 직선의 방정식을 일반화한 형태를 그대로 사용하는 것이고, 이 때 physical depth에 해당하는 차원의 element가 1이게 된다.(그래서 앞서 HC를 정의할 때 f=1로 생각한 형태를 사용한 것이지 않을까. 반대로 2D상의 직선을 표현하려다 보니 결국 f=1이라는 transform을 생각해낸 것이 아닐까)
- 의미
결국 HC를 사용하게 된다면 원래 3D 객체를 2D의 image로 나타내게 되는데, 이렇게 하면 image, target도 모두 3D 상에 존재하는 것으로 처리가능하다! 즉, 일종의 projection하는 대상 공간을 고정시킨 것으로 생각된다.
(아마 이것의 의미가 focal length가 1로 고정시킨다는 것으로 생각해도 될듯?)
Benefits
target의 image를 3D상의 대상으로 만든다는 것은, 결국 그 들간의 상호작용도 수학적으로 모델링할 수 있게 된다.
두 선의 intersection
: cross product of two lines
- Proof(TBD)
두 점을 지나는 직선
: cross product of two points
- Proof(TBD)
직선 위의 점
: dot product of line & point
- Proof(TBD)
Linearity
Translation and rotation, which is rigid body transform, are both linear.
Projection
Once we can formulate HC coordinates, we can consider projection as a linear transform either.
Perspective Model
앞서 HC를 통해 일종의 추가 차원을 늘리는 효과는 결국 두 대상에 간의 상호작용부터, transform까지 안정적으로 기술할 수 있게 되었다.
이제 기존의 환경으로 돌아와서 생각해보면 우린 3D상의 대상을 2D에 위치하게 만들고, 이 2D를 좀 더 편하게 다루기 위해서 HC를 사용해 3차원의 대상으로 다루고, 이렇게 만든 원래 2D였지만 3D가 된 대상 간의 interaction도 잘 정의하게 되었다.
더 나아가서 원래 3D였던 대상도 HC로 접근하는 경우에는 일종의 4D로 서술할 수 있으며, 원래 관심을 가지던 3D에서 2D로 projection을 하게 되는 것은 4D에서 3D로 projection을 하는 것으로 볼 수 있다. 즉 (3*4)의 Linear Transform을 정의하고 싶어진 것이고, 이에 대한 formulation이 바로 perspective model이다!!
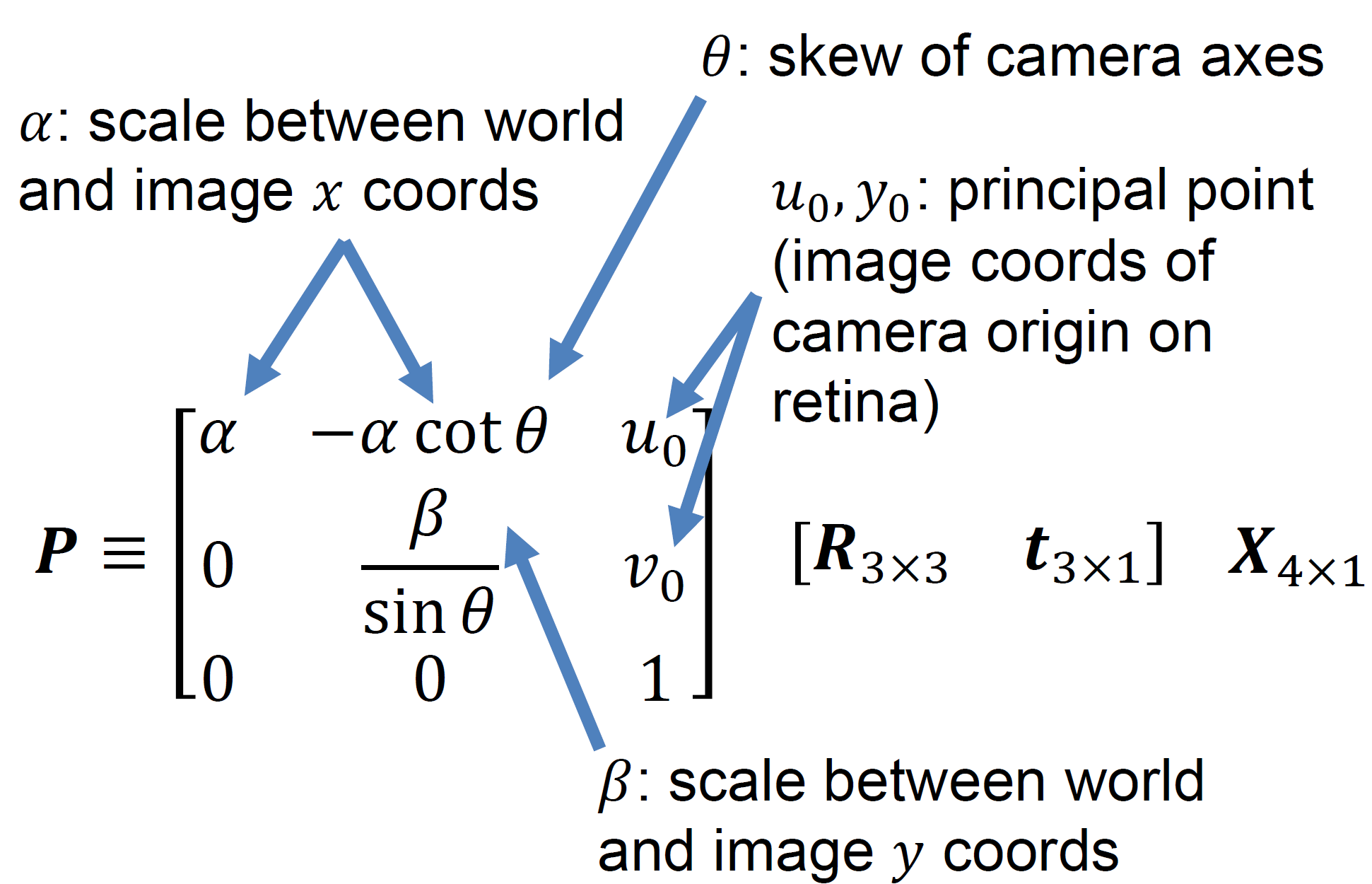
Matrix formulation-Typical Perspective Model
결국 우리가 3D의 target $X$에 대해서 focal plane 상에 맺히는 image를 $P$라고 했을 때, 위와 같이 정의할 수 있게 된다.
-
Extrinsic Matrix 이는 실제 3D공간과 카메라 간의 정렬을 위해 Rotation과 translation을 진행하는 것
-
Intrinsic Matrix 2D상에서 focal length 만큼 scaling함과 동시에 카메라와 image의 좌표를 align하는 principal point($u_{0}, y_{0})만큼 translation을 하게 된다.
여기서 principal point가 $(0,0)$이라면 실제 카메라와 image의 중심 좌표가 동일하게 되는 것이다. (아마 이러한 align이 필요한 것은 흔히 optics에서 optical axis와 align 되어 있는 것을 고려하기 때문에 동일한 작업을 진행하게 되는 것!)
Matrix formulation-Full Perspective Model
$\alpha$와 $\beta$는 각 image coordinate의 axis에 대한 focal length를 표현한 것이고 typical을 보다 더 일반화한 경우에 해당한다.
Orthographic
z축을 그냥 무시하기 위해 z=0으로 만드는 것! focus에 무관한 구조를 가지게 된다는 것이니 어디에서 보든 동일한 뷰가 되도록 하고 그래서 parallel한 것들도 image상에서 parallel하게 되는 것으로 생각된다!(z=0이라는 것은 focal length가 0이라는 것이고, 이건 pinhole model로 접근하는 게 아니라 빛이 들어오는 그 자체를 바로 본다고 생각하는 것이지 않을까)
Thin lens Model
결국 lens를 통해 빛이 들어오는 환경을 고민해볼 때 몇가지 특징을 가진다.
- 렌즈의 중심을 지나는 빛은 그대로 진행한다.(영향을 받지 않는다.
- 평행광은 렌즈를 통화하고 focus에 빛이 모이게 된다.
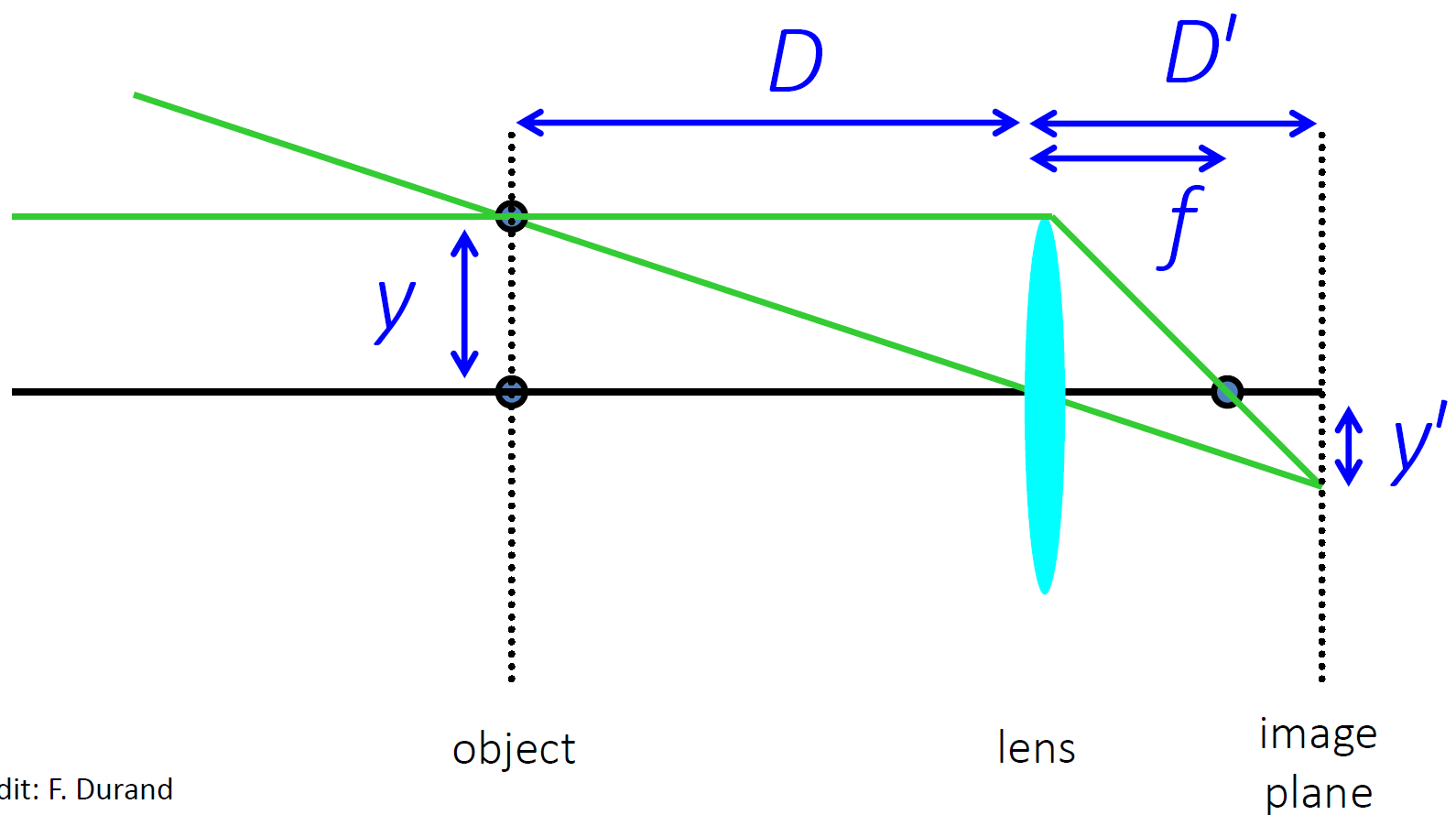
Formulation
- eq 1
${y’ \over D’-f} = {y \over f} \Leftrightarrow {y’ \over y} = {D’-f \over f}$
- eq 2
${y’ \over D’} = {y \over D} \Leftrightarrow {y’ \over y} = {D’ \over D}$
- eq 3 (Mirror equation)
${D’ \over D} = {D-f \over f} \Leftrightarrow {1 \over D} + {1 \over D’} = {1 \over f}$
Depth of Field(DOF)
결국 우리가 관심있는 것은 object를 focus에 맞추고 싶은데, 주어진 configuration($D’, f$)에 얼마나 깊이 혹은 얼마나 멀리 focus가 맞는지 알려주는 것이 DoF다!
- Aperture
렌즈의 aperture를 줄이게 되면 결국 빛이 좀 더 모이게 된다! 이를 이용해서 outfocus와 같은 효과를 만들기도 한다.
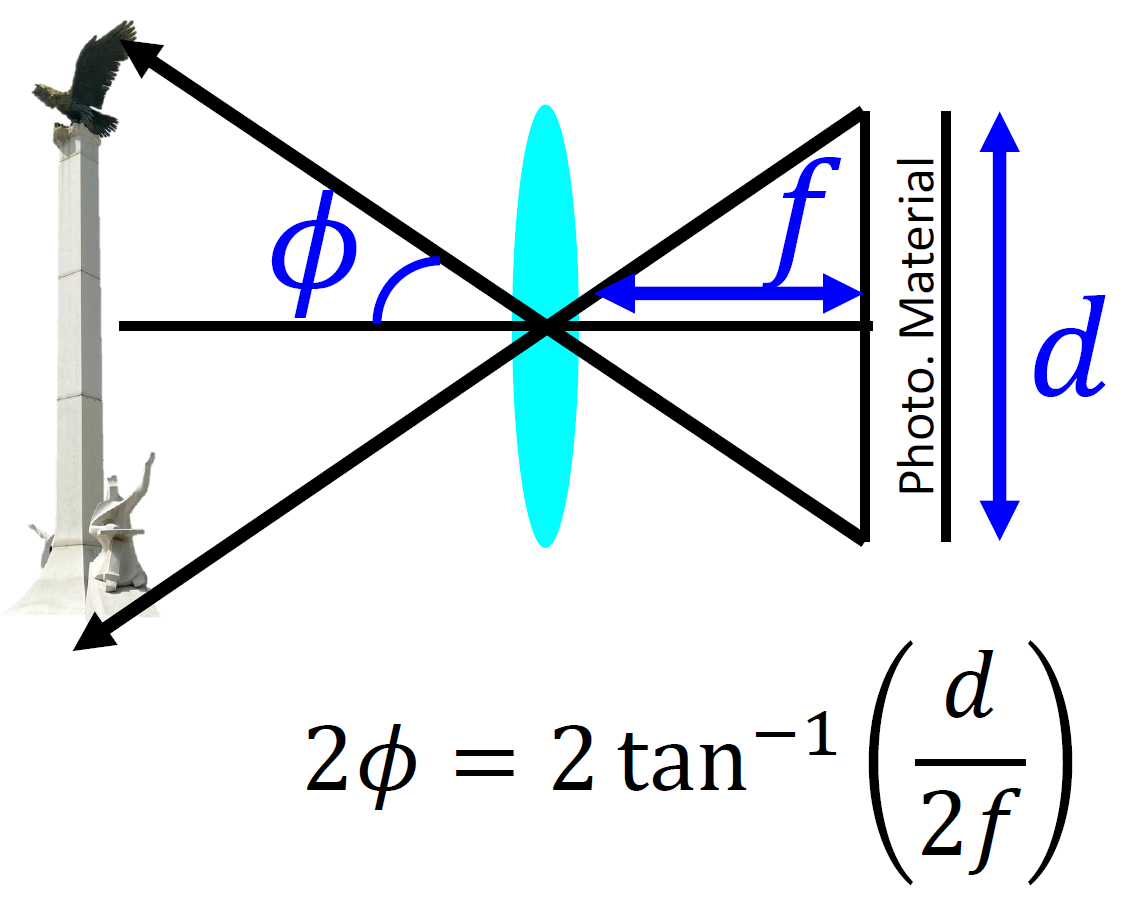
Field of View(FoV)
얼마나 멀리 볼 수 있게 하는가? 시야각을 넓히기 위해선 결국 focal length를 줄여야 한다!
반대로 focal length가 커서 FOV가 줄어든다고 하면 멀어질수록 distortion이 커지게 된다.
Limitation
Pin hole 모델에서 Thin lens model로 넘어가면서 생기는 이슈들이 있다.
- Radial Distortion: optical axis로부터 멀어질수록 휘어져 보인다.
- Vignetting : 중심으로 부터 먼 빛들은 점점더 어두워 진다.(빛이 덜 들어가니)
- (Chromatic) Aberration: index of refraction이 파장에 따라 달라지는 것을 얘기.
- Rolling shutter

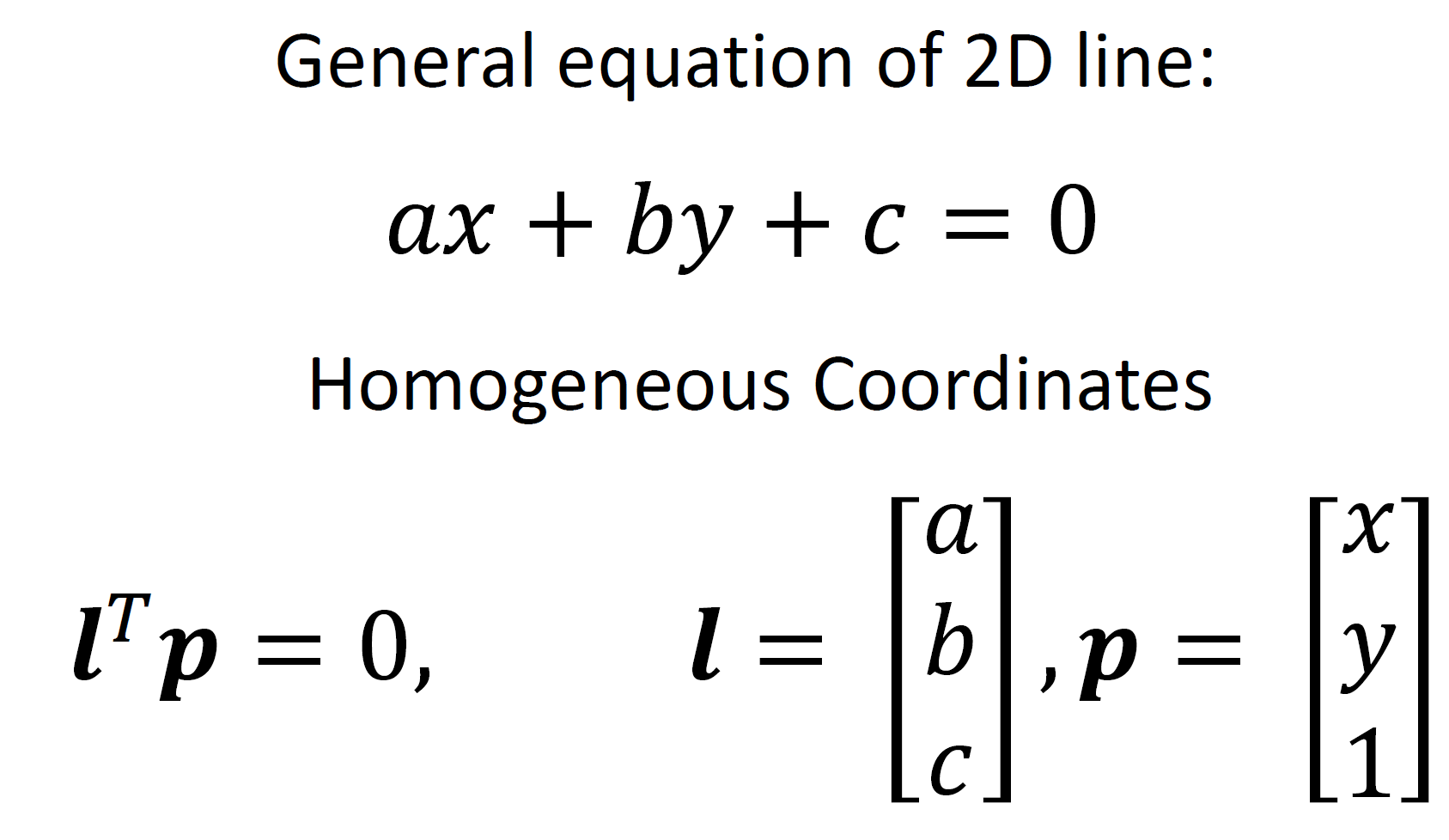


댓글남기기