[Lecture] Filtering: Computer Vision for Data Science
Convolution
주어진 픽셀 값들을 이용해 pixel 값을 계산(혹은 업데이트)하는 것으로, neighbor pixel들에 대해서 일정한 weight를 가지고 avg를 구하는 것!
- 이 때 weight에 해당하는 것이 filter kernel
- 이렇게 처리하면 결과 이미지의 크기는 줄어들게 된다.
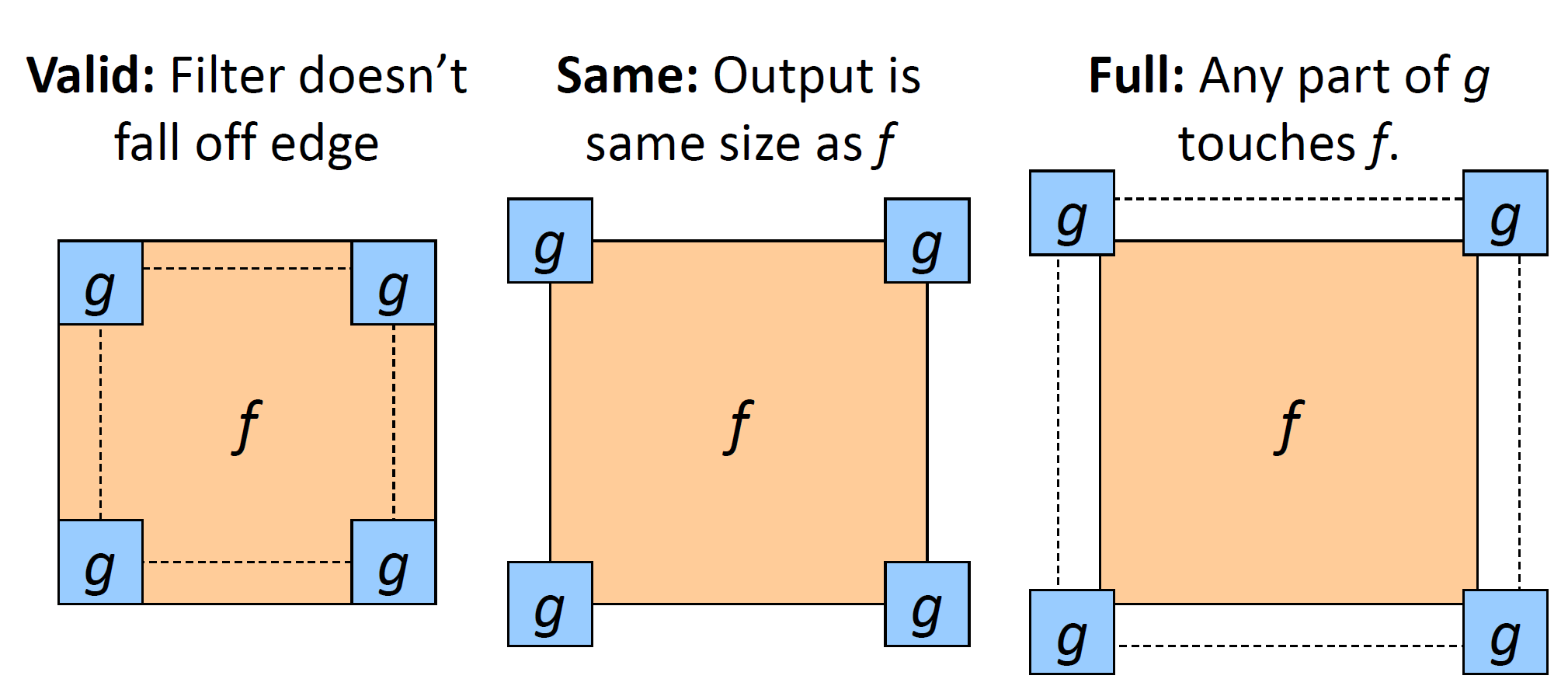
Edge case
결국 convolution을 하게 되면 edge에서 값의 처리가 문제가 되고, 이를 해결하는 방법은 총 3개가 있다.
- 우린 same edge case를 이용한다! 여기서 특징은 이미지 외부에 filter를 사용하는 것도 용인하게 된다.
- full case는 image pixel이 하나고 그 외엔 전부타 fall off가 되더라도 허용하는 것을 말한다.
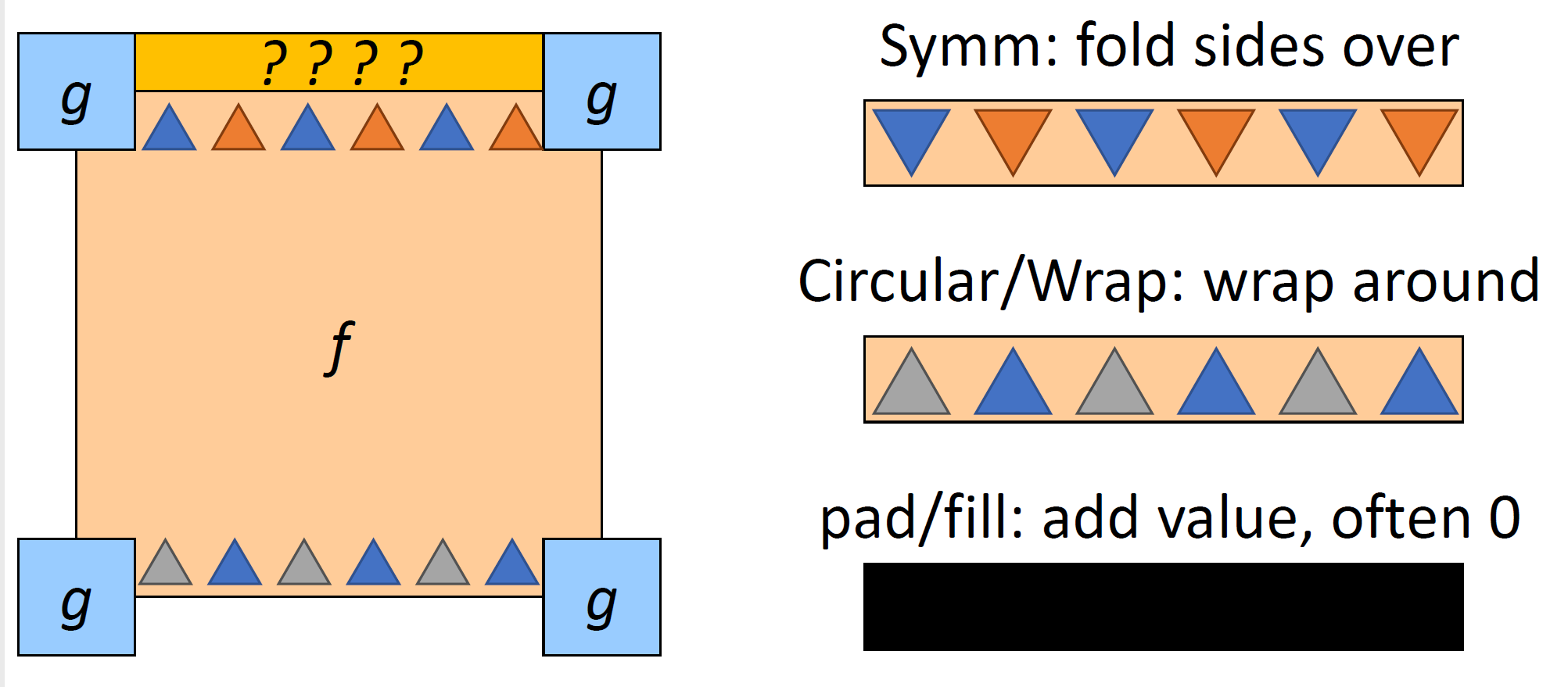
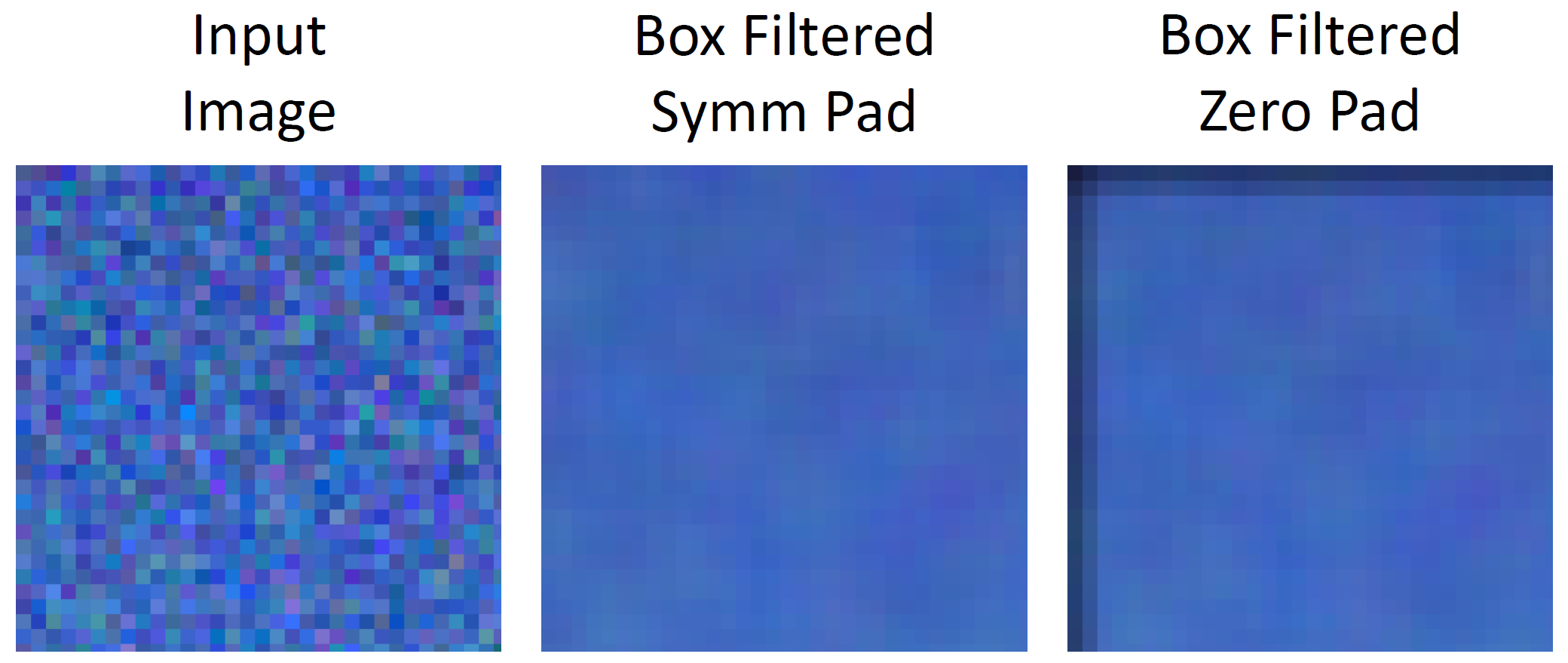
how to pad?
어떻게 padding을 하는지에 따라서 output이 달라지게 될 것이다!
Linear Filters
결국 filter를 어떻게 구성하느냐에 따라서 결과물이 달라지니 filter들을 정리해보자
Cases
-
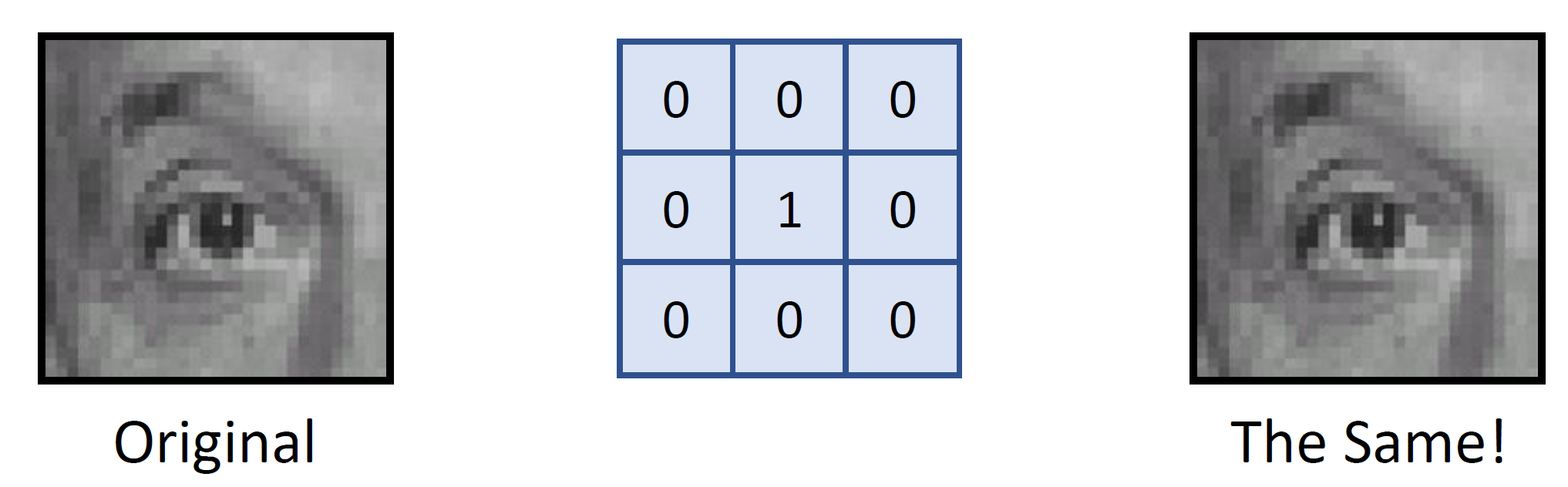
Identity
-
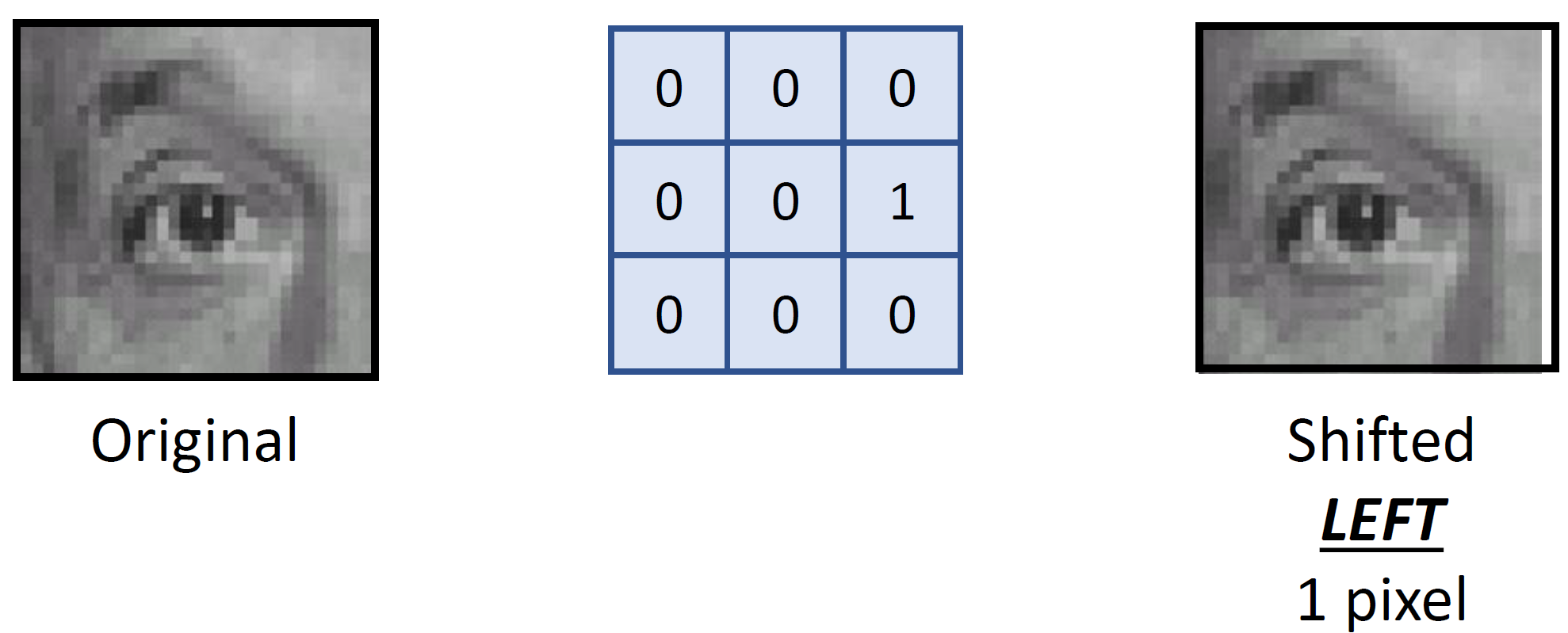
Shift
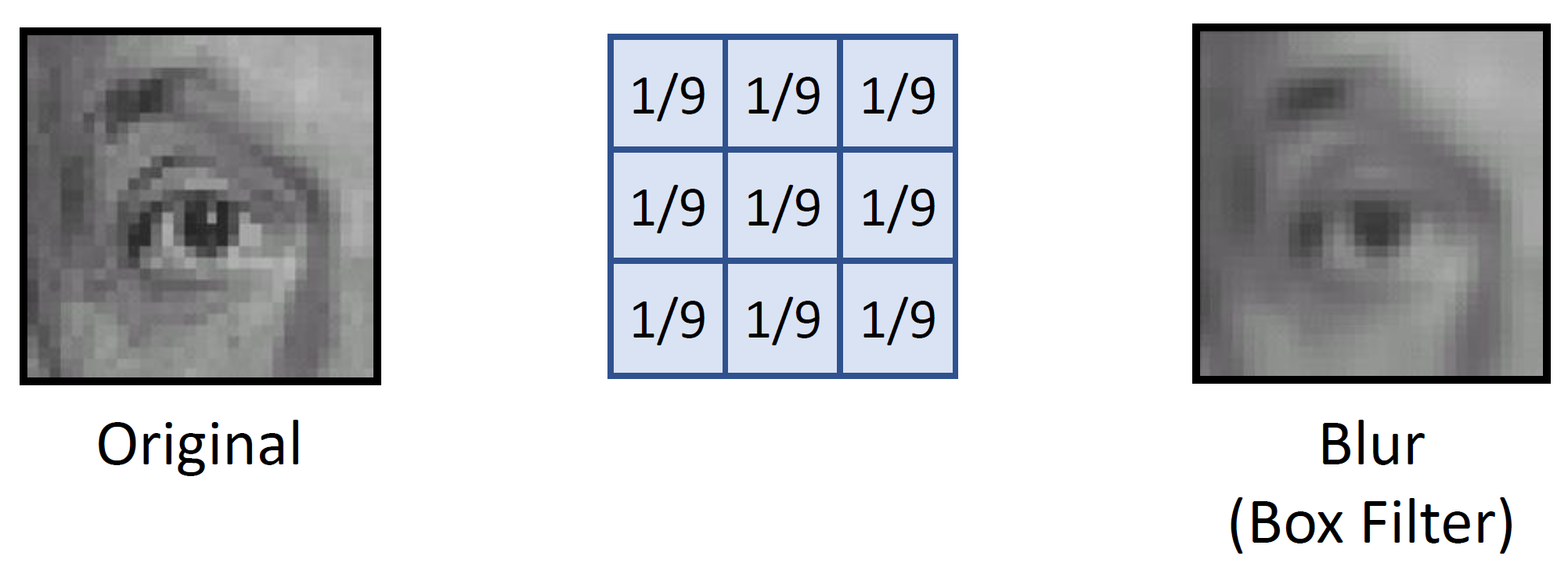
- Blur(box filter)
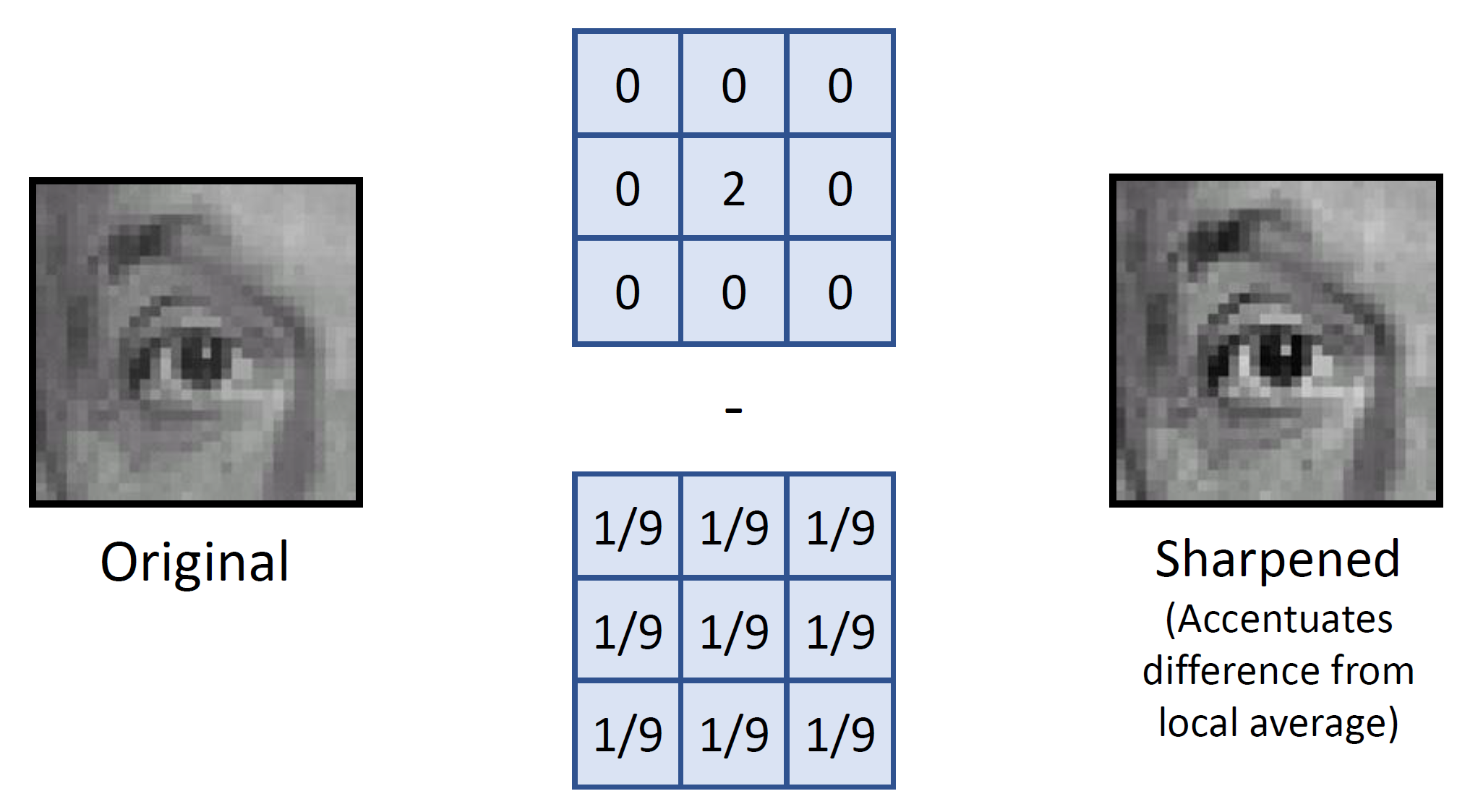
- Sharpened
pixel 값을 강화하고, blur를 빼주니!!
Properties
-
Linearity : 두개의 필터를 합친 것을 한번에 적용하는 것이나 각각 적용하고 더하는 것이나 동일하다!
-
Shift-invariant : 필터를 하고 shift를 하느냐, shift하고 filter를 하든지 동일한 결과. 이는 neighborhood만 고려하는 filter의 특징(즉 locality만 고려한다는 것!)
-
summary
Terminology
실제로 convolution 연산이라고 하는 것은 filter를 flip하고 나서 적용하는 것인데, 지금처럼 바로 계산하는 것은 사실 cross-correlation이라고 한다!
convolution인 경우에만 결국 commutative하게 되는 것
Use case : Box smoothing
사진을 보면 box형태의 artifact들이 너무 많다. 이것을 비슷하게 나타나도록 하는 것이 바로 box smoothing인 것이고, 이런 역할을 하는 것이 box-filter다!
그런데 꼭 uniform한 weight를 가질 필요는 없고 좋은 방법은 무엇일까?
Per Pixel Weight: Gaussian
이것의 아이디어는 filter의 중심으로 부터 멀어질수록 감쇄가 되는 filter를 가진다는 것!
특히 이렇게 그냥 proportion형태로 나타낸 것은 결국 filter size에 finite하니 이것에 대해 normalize를 해야하기 때문에 equality로 나타낼 필요가 없다.
또한 gaussian filter에서 $\sigma$ 값을 어떻게 조정하는지에 따라서 형태가 달라질 것!
다만 이렇게 하게 된다면 filter size와 $\sigma$ 간 균형이 중요한데, filter size가 커질수록 computational expensive하게 된다!
- 적절한 filter size는 $6\sigma$ 로 하는 것
특히 이런 gaussian은 특정 frequency 이상에서의 noise를 지워주는 효과가 있게 된다.
Seperable Filters
앞서 언급한 바대로, 2D filter는 연산에 있어서 time complexity가 문제였다.
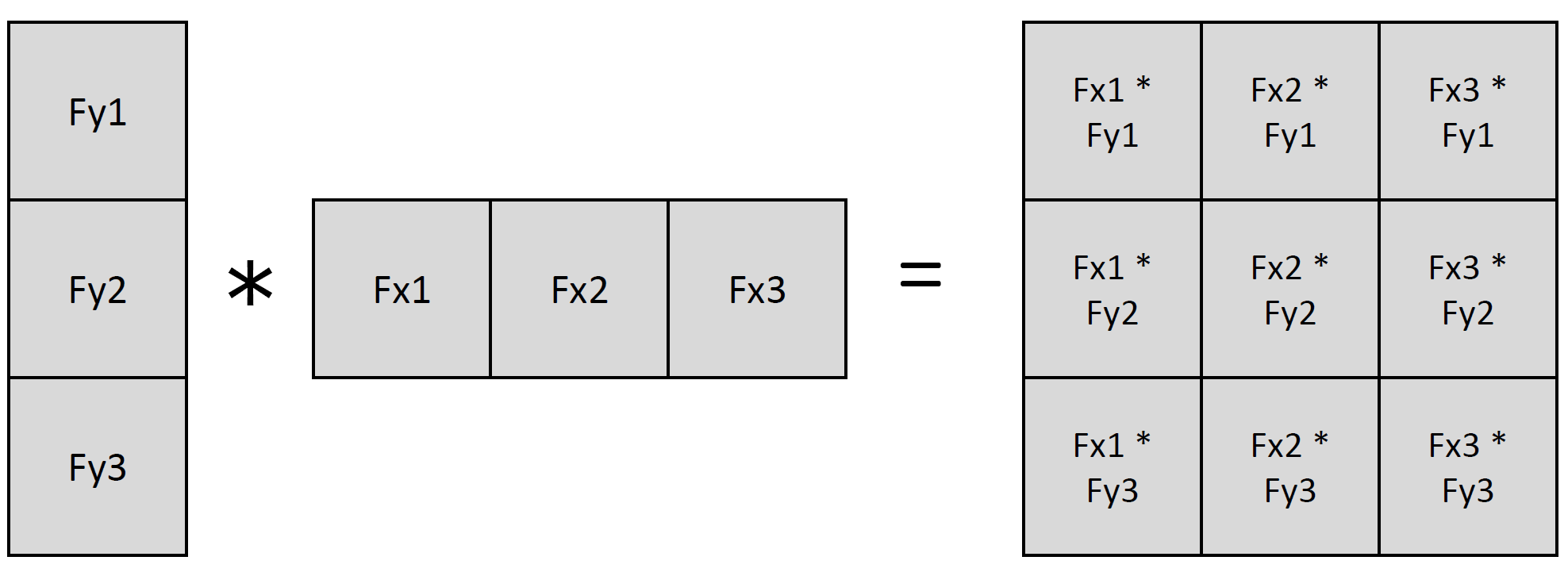
그래서 2D의 convolution filter를 1D convolution filter의 outer product으로 처리하는 것!
- 이 때 우린 full convolution with zero-padding을 가정
- 또한 filping을 무시한다(cross-correlation을 이용)
수식적으로는 두 exp의 곱으로 나타내면 쉽고, 이를 convolution 연산의 linearity(특히 associative)를 이용해서 변형이 가능하다.
그럼 다음과 같이 time complexity가 개선된다.


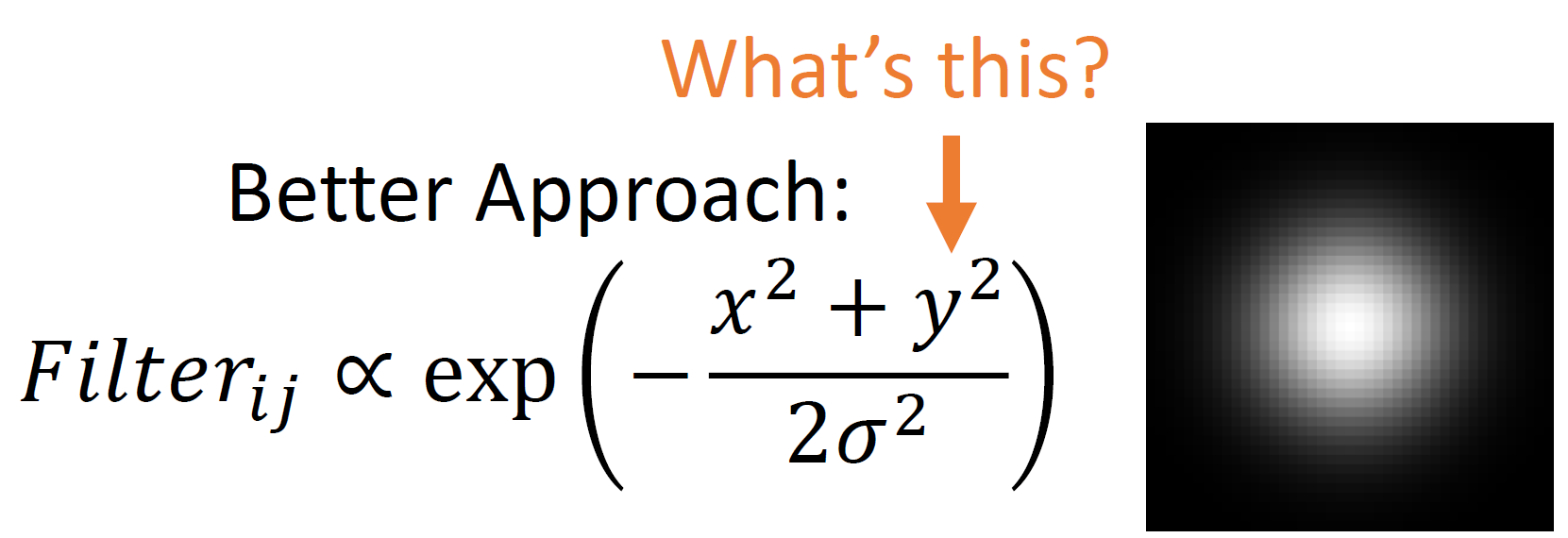



댓글남기기