[KMOOC 강화학습] Week 04-1 Markov Process Overview
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
Markove Decision Process
- 확률적 동적 계획법: 동적 계획법 + 마르코브 프로세스
근본적으로 불확실성을 내포하고 있고, 이를 수학적으로 모델링하기 위해 확률의 개념이 들어오는데,
우리가 기본적으로 확률 변수와 확률 분포를 통해 시스템의 불확실성을 표현하며, 시간에 따라 확률적으로 변화하는 프로세스를 다루는게 중요한 것!
- 예시: 날씨
날씨를 3가지 카테고리로 나눠서 생각하고, 각각의 확률로 나타낼 수 있을 것이다!
이런 상황에서
- 기본적으로 날씨는 시계열이며
- 내일의 날씨와 오늘 날씨간 상관관계가 존재할 것이니 시간의 흐름에 따라 불확실성이 변동할 것
- 예시 : 전염병 분석
공통적으로 일정 부분 증가후 감소하는 특징이 있고, 이를 수학적으로 모델링을 해본다면,
현재까지 확진자수 이력을 바탕으로 다음 추가 신규 확진자 수는?
확률 과정(stochastic process)
확률적으로 변화하는 프로세스를 모델링하기 위해 수학적으로 접근하는 방법으로, random process와 stochastic process가 있다.
Problem Formulation & Definition
- 즉, 시간에 따라 이벤트의 확률값이 변화하는 것이 stochastic process라고 하고
- 여기서 불확실성을 모델링하기 위해 확률과 확률변수를 사용하며
- 각 시점을 하나의 확률변수라고 할 때
-
시간에 따른 확률변수들의 집합이 된다.
- 이때, 결합확률분포(join probability distribution)을 정의하며
- 시점들의 집합을 시간공간(Time space)이라고 하며
- 확률변수들이 어떤 값을 가지는 값을 상태라고 하며
- 이 때 확률 변수가 가질 수 있는 모든 가능한 값들의 집합을 상태 공간이라고 한다.
즉 시간이 진행함에 따라 상태가 확률적으로 변화하는 과정을 확률 과정이라고 한다!
예시 : 동전던지기
- 확률 변수 $X_{n}$ : $n$번째 동전을 던졌을 때까지의 누적 점수
- 상태 공간 $S$ = {…, -2, -1, 0, 1, 2, …}
- 시간 공간 $T$ = {0, 1, 2, …}
종류
- 이산 시간- 이산 상태 : 우린 이거 포커스
- 연속시간 - 이산 상태
- 이신시간 - 연속 상태
- 연속시간 - 연속 상태
결국 이렇게 하고 나서 예측을 하고자 한다! 다음 단계의 상태를 예측하고 싶은 것.
우리가 결합확률 분포를 조건부 확률의 곱으로 표현이 될텐데, 조건부 확률를 정의하고 사용할 것이고 이게 중요하게 된다!
개념
sample path : episode
확률과정의 실현치들의 샘플을 모아둔 것으로 일종의 시계열 데이터 샘플을 말한다.
stationary process : 정상 과정
시간에 따라 확률 법칙이 변하지 않는 확률과정으로 시간이 변하더라도 상태 확률이 변하지 않는 과정
Modelling
기존의 데이터가 주어졌을 때 다음 단계의 확률을 알고 싶은 것이고 이게 바로 조건부 확률
- 과거와 완전히 독립적인 경우: Independence assumption
- 시간의 흐름과 관계가 없기에 굳이 분석할 필요가 없다.
- 현재만 미래를 결정하는 경우: Markov Process
- 가장 단순한 형태로, 현재 상태만 의존한다!
-
ex. P(future present, past) = P(future present) : Markove property
- Time space가 discrete한 경우 : Discrete Time markov chain(DTMC)
DTMC
조건부 확률로 결합확률을 계산하고자 하고, 마르코브 성질을 만족하게 되니 이산사건 마르코브 프로세스라고 한다.
여기서 chian이라는 말의 의미는 상태 공간에 속해있는 값들이 셀 수 있는 경우를 말한다. 즉 확률 과정이 셀 수 있는 대상들 중에서 하나를 고르는 경우를 말하는 것.
| $P(X_{n+1}=j | X_{n}=1,.X_{n-1},…) = P(X_{n+1}=j | X_{n}=i)$ |
state transition probability
| $P(X_{n+1}=j | X_{n}=i)$ |
이를 상태 전이 확률(1-step stae transition probabiltiy) : $i$상태에서 다음단계가 $j$가 될 확률이라고 하고,
단계별 정의 가능: 다른 단계에서 상태가 둘 다 $i$라고 하더라도 확률이 다를 수 있다.
즉 단계마다 원래 확률이 다 정의해야 한다.
Time-homogeneou DTMC
만약 어떤 단계든 독립적으로 동일한 경우라고 가정한다면, 전이 확률이 $n$에 독립적인 것으로 어떤 단계이든 무관히 어떤 상태가 되면 항상 독립적이다. 즉 시간에 독립적으로 확률이 나오게 되는 것이다.
즉 현재 $i$상태라고 할 때 그 다음이 $j$가 될 확률은 시간에 독립적으로 동일한 것이다!
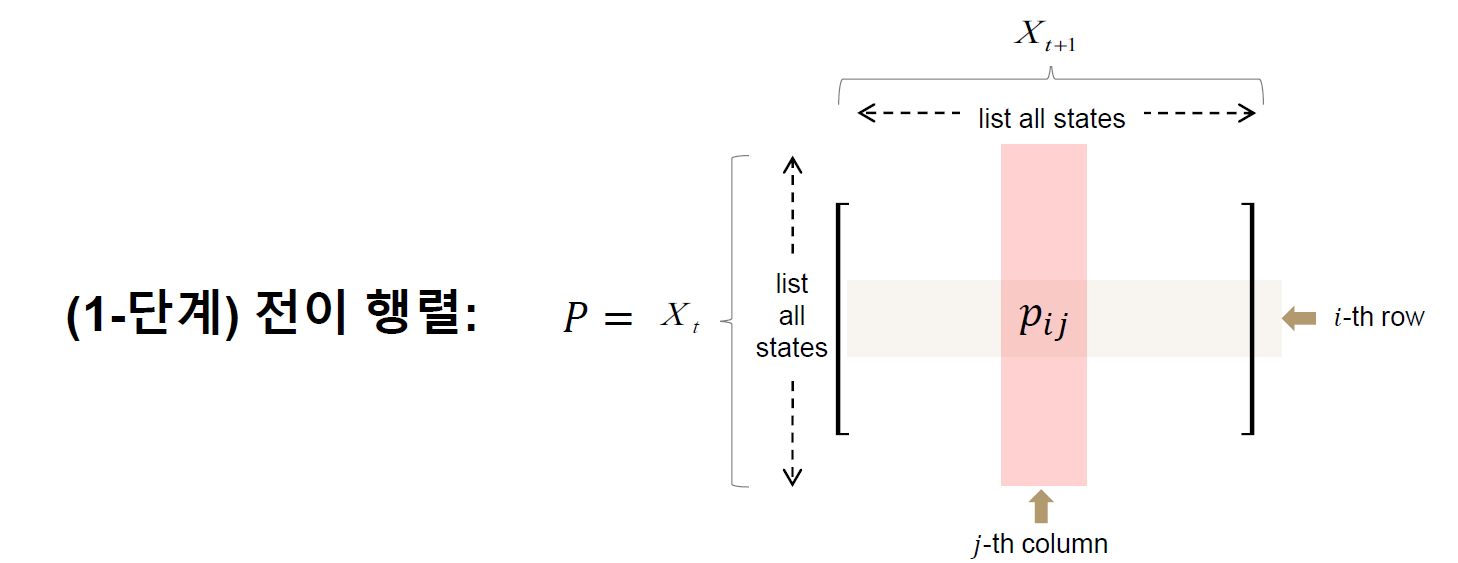
이런 정의에서 하나의 행렬(어떤 상태에서 다음 상태가 될 확률로 표현)만 있으면 Markov Process를 분석가능하다. 이 때의 행렬을 (1-step) 전이 행렬이라고 한다.
댓글남기기