[KMOOC 강화학습] Week 06-1 MDP Value Function
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
MDP는 동적계획법 중 stochastic 이며 시간공간, 상태공간, 행동공간, 상태전이확률, 보상로 구성되어있다.
순차적인 의사결정이란 좋은 선택을 위한 판단근거가 필요하고, 보상이라는 정보를 활용한다. 그래서 뒤에 이어질 보상까지 고려해서 의사결정을 내리고자 하고 이를 정의하는 것이 가치함수다.
가치함수란
상태 가치 함수(State-value function)
매 의사결정 시점마다 모든 상태에 대해 어떤 행동을 취할지 알려주는 함수, 혹은 확률분포의 집합이다.
다음의 식은 Bellman Expectation Equation이라고 하며 어떤 시점 t에서 상태가 s일때 정책 $\pi$ 를 따른 경우의 남은 기간동안의 얻을수 있는 누적된 보상, 리턴에 대한 기대값이다.
참고로 마코브 보상 프로세스에서 가치함수를 정의하는 것과 동일한 개념이며 우리가 finite horizon의 경우에는 감가율을 1로 두지만 일반적인 상황에 대해 서술한 식인 것이고, 미래에 얻을 보상을 현재가치로 변환했을 때의 보상들의 총합이다.
행동 가치 함수(Action value function)
위의 식은 어떤 시점 t에서 상태가 s일때 행동을 a를 취하면 다음상태로 전이 되고, t+1시점에 정책 $\pi$ 를 따를 때의 누적 기대 보상합에 대한 기댓값이다. 중요한 것은 $R_{t}$ 는 행동 a에서 기인한 것이고, 그 이후의 보상들은 정책 $\pi$ 를 따르면서 얻은 보상이며 그렇기 때문에 a에서 $\delta$ 로 바뀐 것을 사용한 것이다.
차이점으로 $R_{t}$ 는 행동 a에 의해 결정되고, $R_{t+1}$ 은 $\pi$ 에 의해 결정되는 누적 보상합을 말한다.
서로간의 관계
행동 가치 함수는 지금 단계에서의 행동을 하고 그 이후는 정책을 따르는 것이며 상태 가치함수는 지금 시점도 정책을 따르는 것이기 때문에 다음과 같은 식을 만족한다.
여기서 중요한 것은 $\delta_{t} (a\mid s)$ 는 상태 s에서 a라는 행동을 취할 확률을 말하기에 위와 같은 식으로 서술되는 것이다.
예시
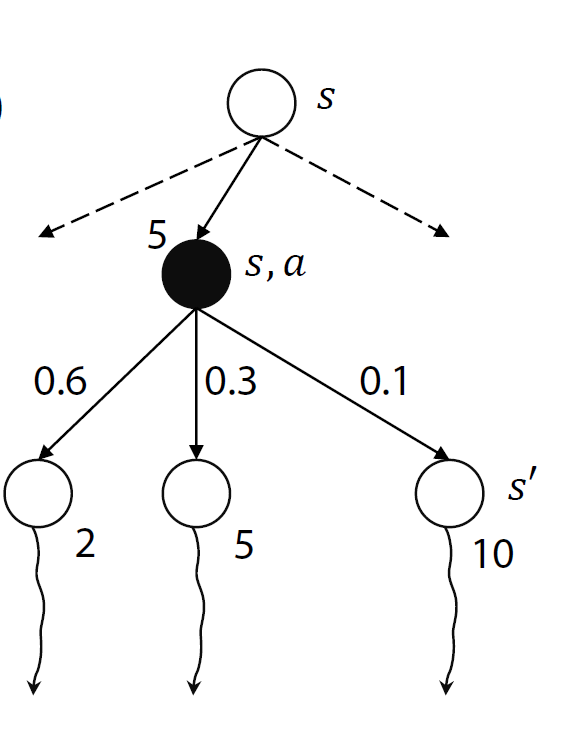
위의 식에서
- 현재 a라는 선택을 하면서 얻게 되는 보상 5
- 그 다음 단계부턴 감가율을 고려하고
- 그 상태에서 다음 상태로 갈 확률과
- 그 상태에서 다음상태로 전이할 확률들의 곱들의 합
재귀식 정의
상태 가치함수의 재귀식
앞서 서로간의 관계식을 통해서 재귀식을 정의할 수 있다. 이 때 행동 a 대신에 $\delta_{t}(s)$ 를 사용하게 되면 얻게 되는 식이다.
행동 가치함수의 재귀식
최종 목적
누적 보상합을 최대화할 수 있는 정책을 찾고자 한다!
최적 정책(optimal policy)
finite horizon의 경우,
모든 $s\in S$, 모든 $\pi$ 에 대해
$v_{1}^{\pi^{*}} >= v_{1}^{\pi}$
최적 가치 함수
감가율이 반영된 기대 누적보상합의 최대값으로 다음의 식으로 정의된다.
$v_{1}^{*}(s) = \max_{\pi} v_{1}^{\pi}(s)$
이 때 최적 정책을 가진다면 최적 가치함수와 최적 정책은 모든 상태에 대해 동일하게 된다.
계산 방법: Bellman Optimality Equation
확정적 동적 계획법에서의
지금 단계에서의 보상과, 다음 상태로부터 얻을 수 있는 누적보상합의 최대값의 합으로 다음과 같이 정의된다.
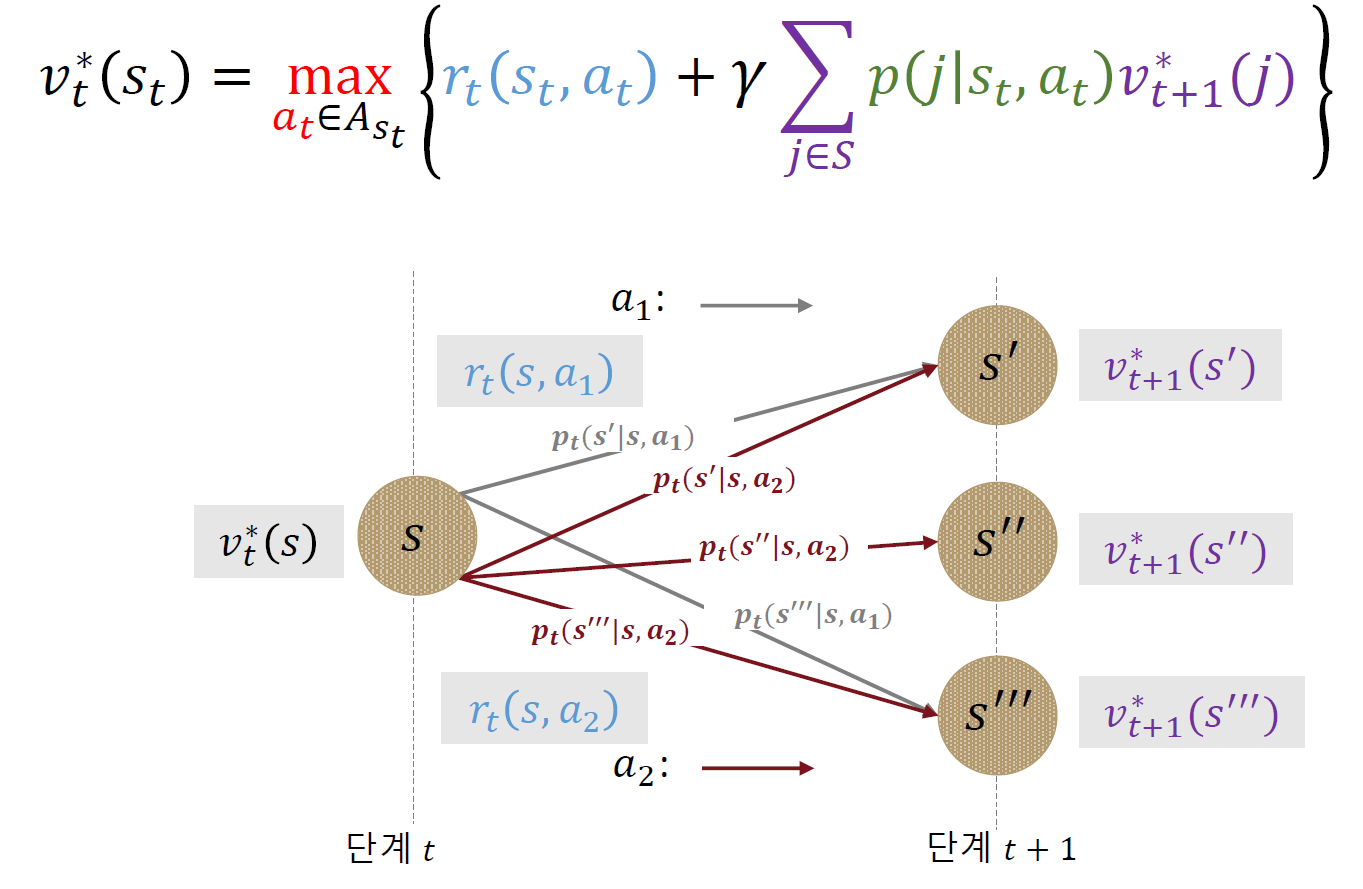
MDP에서의
여기서는 확률의 개념이 들어가 기대값으로 계산이 된다.
예시
이렇게 문제를 모델링한 다음, 역진 귀납법(backward induction)을 통해 구하면 된다.
finite horizon의 경우 terminal reward가 존재하므로 마지막 상태에서 보상을 계산
$t-1\gets t$ 으로 넘어가 모든 상태에 대해 가치함수를 계산
$t=1$ 까지 계산
이렇게 역진으로 각 단계에서의 행동들을 찾고 이걸 모은 것이 최적 정책이다!
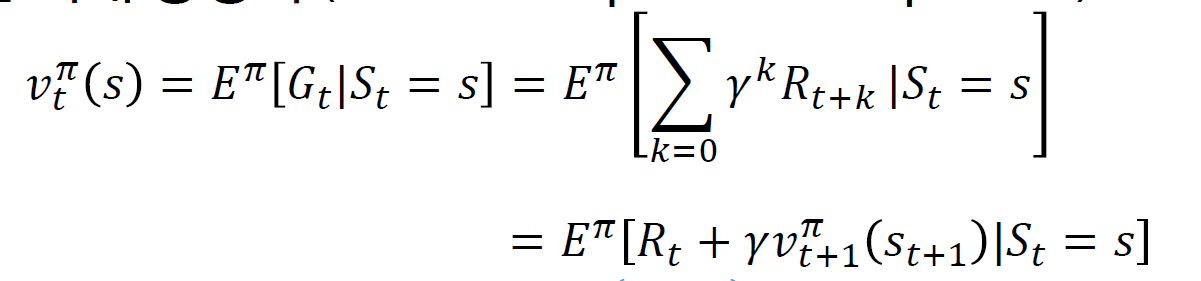
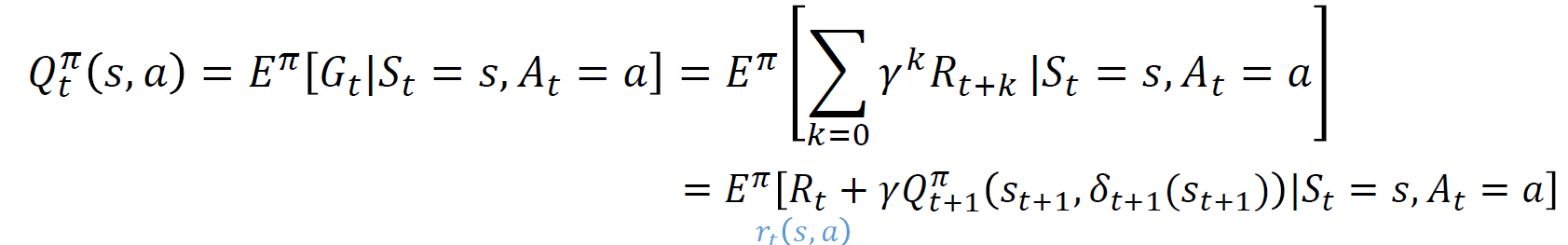
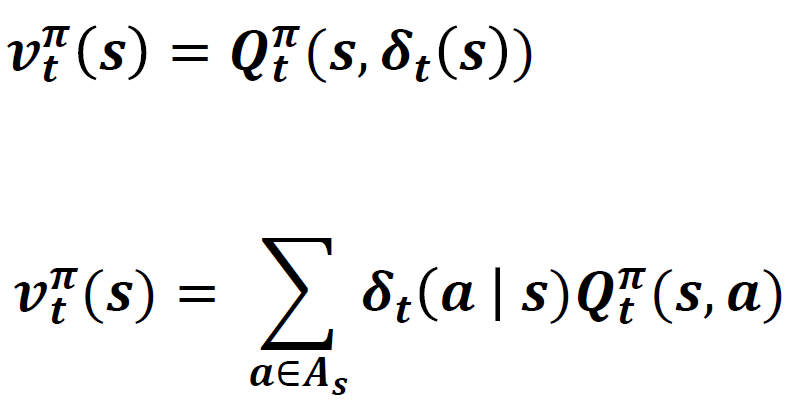
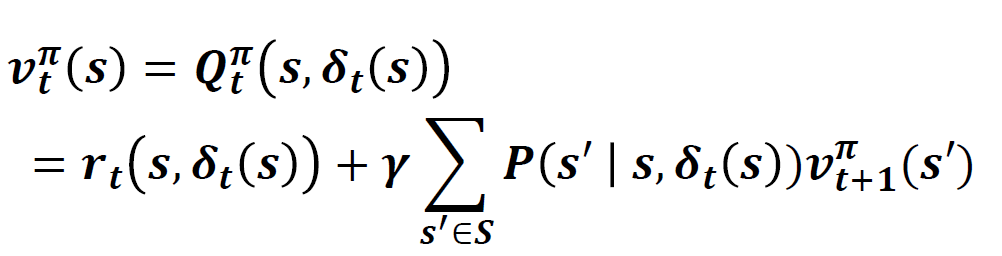
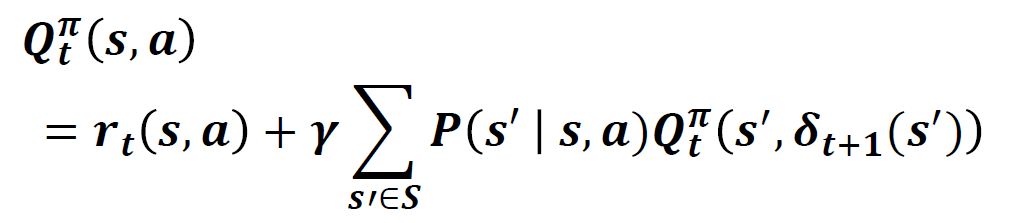
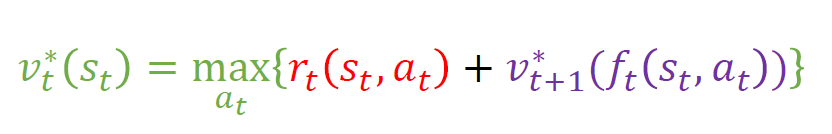
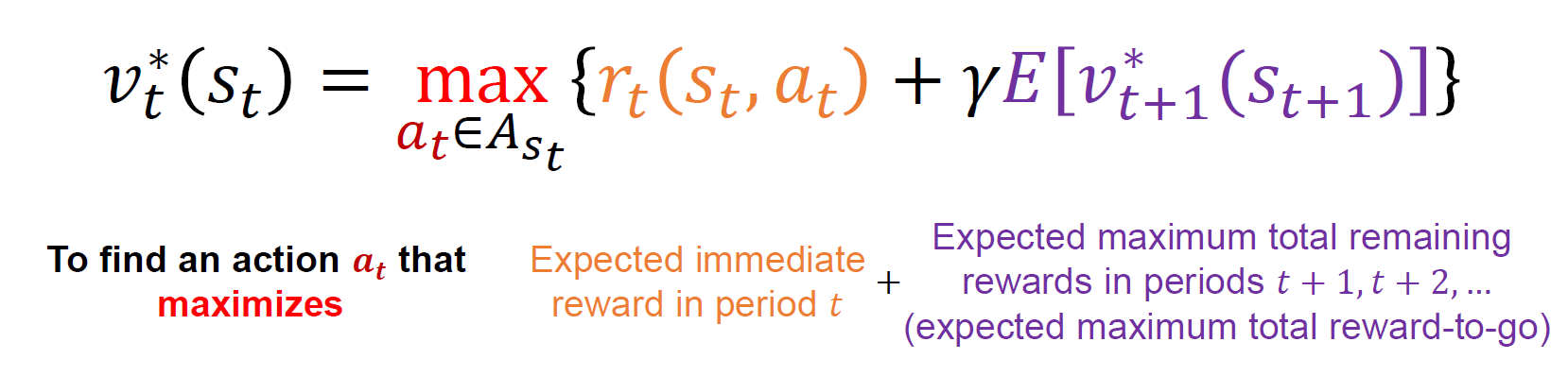
댓글남기기