[KMOOC 강화학습] Week 06-2 Infinite horizon MDP
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
기존에는 finite horizon 문제를 풀었다면 이번 시간에는 끝이 없는 상황을 고려해보기로 한다.
Infinite horizon MDP
강화학습에서 이 모델을 근거로 하고 있다. 이런 과정이 무한히 진행되는 상태를 가정한 것으로, 이걸 푸는 것이 모델 기반의 강화학습이라고 하게 된다.
가정
Stationary 가정
무한히 지속되지만 의사결정단계에 따라 상태 전이 행렬이 바뀌지 않는다! 즉 동일한 상태, 동일한 행동을 취하면 얻게되는 보상은 동일하다.
이런 가정에서 infinite horizon MDP 모델에서 최적의 정상 정책이 존재하는 것이 수학적으로 증명되어 있다.
정상 정책이란
$\pi = (\delta_{1}, \delta_{2},…)$
위와 같이 정책이 정의될 때 동일하더라도 행동이 달라질 수 있기에 서로 다른 $\delta$ 를 사용한 것이 기본 가정이다.
그런데 정상성 가정을 한다면 최적 정상 정책(optimal stationary policy)가 존재한다는 것이므로
$\pi = \delta^{\infty}$ 가 된다.
이런 상황에서 다음과 같은 표기를 사용한다.
$\delta(s) \Leftrightarrow \pi(s), \delta(a\mid s) \Leftrightarrow \pi(a\mid s)$
가치함수
상태 s에서부터 정책 $\pi$ 를 따랐을 때 기대 누적보상합은 다음과 같다.
infinite에서 감가율이 중요한데, 무한히 반복되기 때문에 발산할 수 있고, 그래서 수렴을 보장하기위한 장치다.
감가율
- 0에 가까워질수록 현재 가치를 중요하게 고려한다.
- 1에 가까워질수록 먼 미래의 보상이 현재 보상만큼 중요하다고 계산하는 것이다.
Bellman Expectation Equation
정책 $\pi$ 가 주어졌을 때 상태 s의 가치함수 $v^{\pi}(s)$
위의 식을 읽을 때 중요한 점은 다음과 같다.
- 현재 보상의 기대치와 상태전이 후 누적보상합의 기대치로 나눠보기로 한다.
- 상태 전이 후의 보상을 계산할 때에는 기대값 계산을 이용하여 전이확률과 전이한 상태에서의 가치함수의 곱로 계산된다.
상태 가치 함수 계산법(정책 평가)
정책이 주어졌을 때 모든 상태에 대한 가치 함수 값을 산출하기 위해서 전이 확률이 정해진 정상성 상태에서 3가지 상태가 존재한다고 할 때 다음과 같은 행렬 방정식을 얻게 된다.
중요한 점은
- process가 무한히 진행된다고 할 때 $V^{\pi}$ 는 같다고 둘 수 있다(?)
- 정책이 주어져있고 정해져 있기에 markov reward process와 동일하다.
최적 가치 함수, 최적 정책
최적 가치 함수는 모든 상태 s에 대해 가치함수들 중 정책에 대해서 최대가 되는 가치함수를 말한다.
최적 정책은 다른 정책들보다 항상 크거나 같은 가치함수를 가지도록하는 정책을 말한다.
그래서 최적 정책을 찾게 된다면 최적 가치함수와 같게 되고, 이는 모든 상태, 모든 정책에 따른 가치함수들 중 최댓값을 가지도록 하는 정책을 선택할 수 있고 이 때 누적보상합의 최대값을 말한다!
Bellman Optimality Equation
목적은 의사결정 정책 혹은 최적 정책을 찾고자 하고 그 근거로 Bellman optimality equation을 recursive하게 정의하여 계산했다.
중요한 점은
- 일단 infinite하기에 시점에 의한 것은 제외
- 이로 인해 우변과 좌변의 가치함수는 동일한 것
- 왜냐하면 무한대로 가는 누적보상합이 둘 다 무한하기 때문에 결과적으로 누적 보상합은 같다고 볼 수 있게 된다
최적 정책 찾기
이렇게 가치함수를 얻었다고 할 때 최대가 되도록하는 행동들을 모아서 최적 정책을 찾으면 된다.
최적 행동 가치 함수
일단 행동 a를 선택한 다음에 그 때 최적 정책을 따름으로 인해 얻게 되는 누적보상합의 기대값이다
이렇게 정의하게 되면 결국
$v^{*} (s) = \max_{a} Q^{*} (s,a)$
$\delta^{*}(s) = argmax_{a} Q^{*}(s,a)$
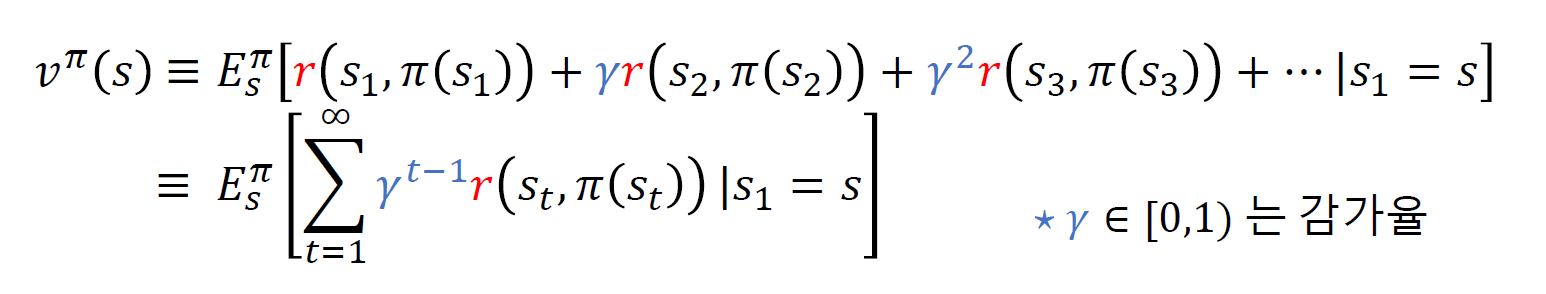
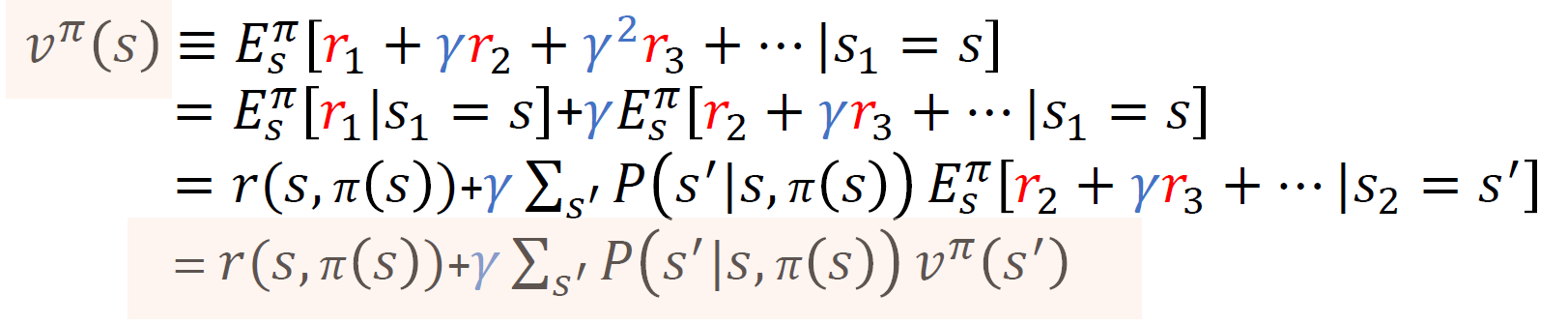
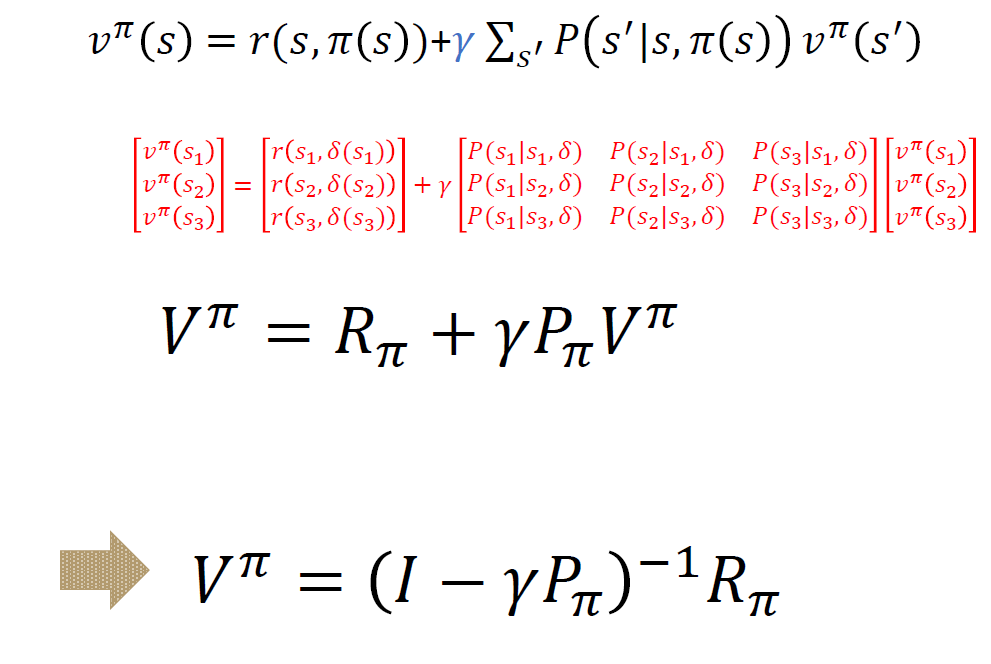
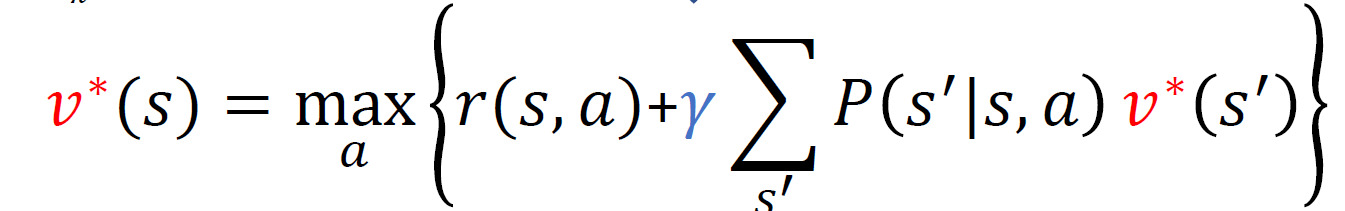
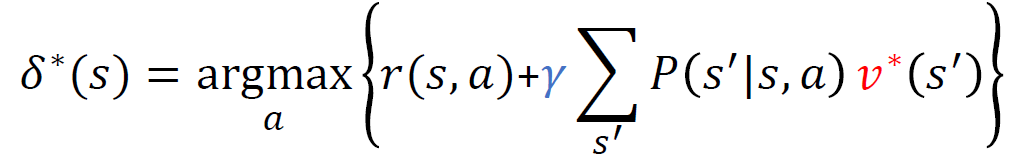
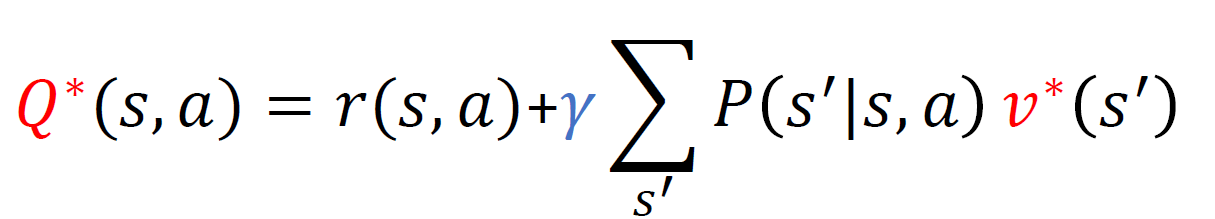
댓글남기기