[KMOOC 강화학습] Week 07-1 Value Iteration
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
Value iteration
기존의 Bellman optimality equation에서 finite horizon은 backward induction으로 풀면 되었고, 이번에는 finite horizon MDP에서 등식을 풀기 위해서 iterative하게 풀고자 한다.
- (k=1) 모든 상태 s에 대해 가치 함수를 0으로 초기화한다(v(s)=0). 사실 임의의 값에 대해서 수렴이 증명되어 있어서 임의로 0이란 값을 할당한다.
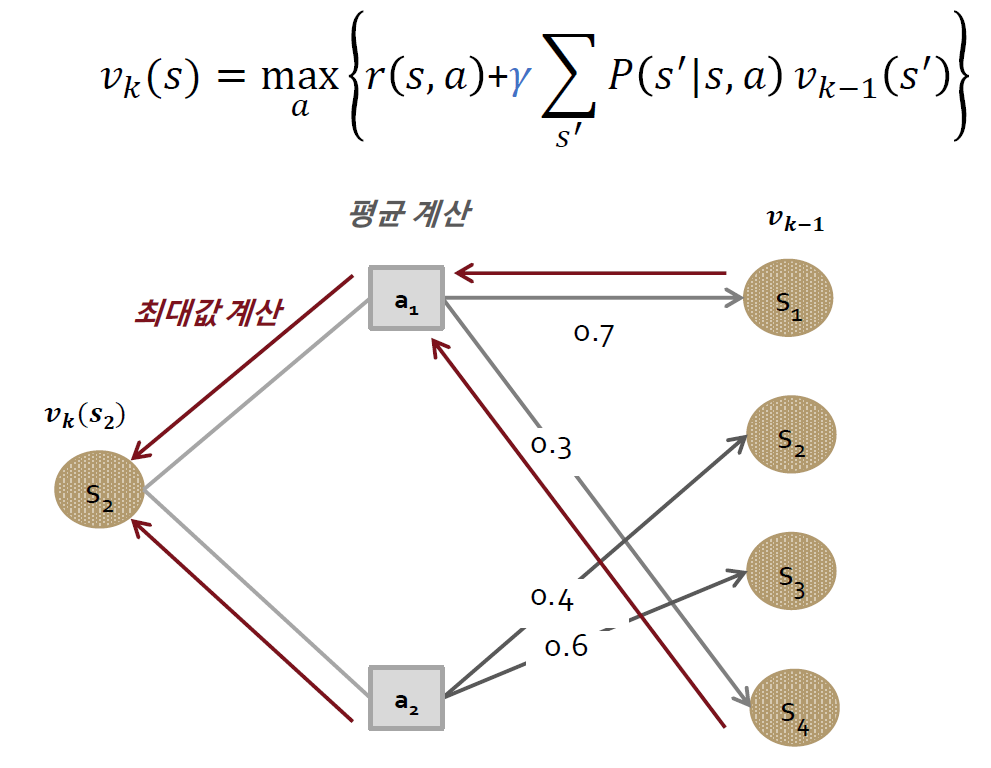
- (k= 2,3,…)이 상태에서 좌변 2번째 항이 0으로 되고 그 때 최대가 되는 a를 찾고 가치 함수 값을 업데이트 하게 된다.
- 모든 s에 대해서 v(k-1)과 v(k) 의 차이가 epsilon보다 작다면 종료하게 된다.
결국 좌변과 우변이 같다는 점을 이용해서 순차적으로 구하게 되는 것이며, 이렇게 하면 항상 수렴한다는 것이 증명되어 있다.
한번 해볼까?
예시
Graph
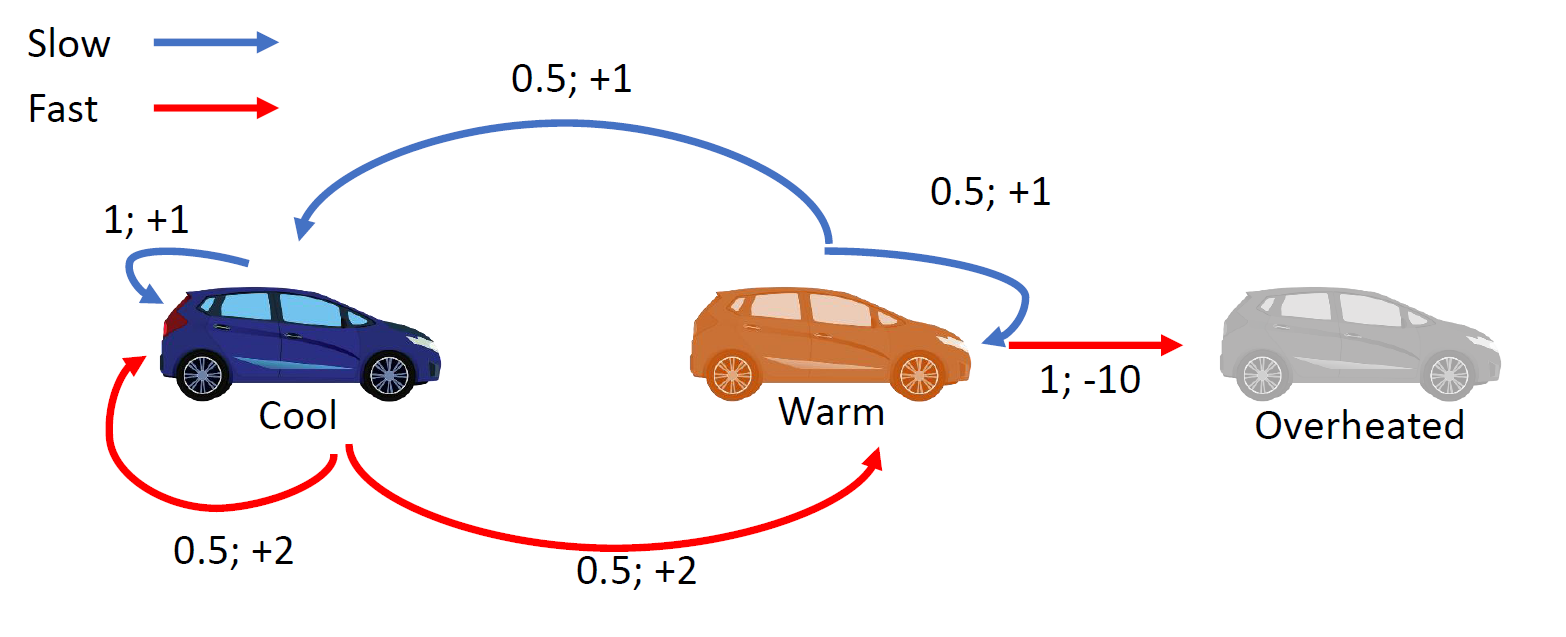
자동차
가정
- Markov Decision Process
- 정상성 가정 만족(상태전이 확률과 보상이 고정)
구성 요소
- 행동 : [Fast, Slow]
- 상태 : [Cool, Warm, Overheadted]
적용
- 모든 상태에 대해 가치함수 초기화
- Step 1
- Step 2
Iteration 한번 해볼까?
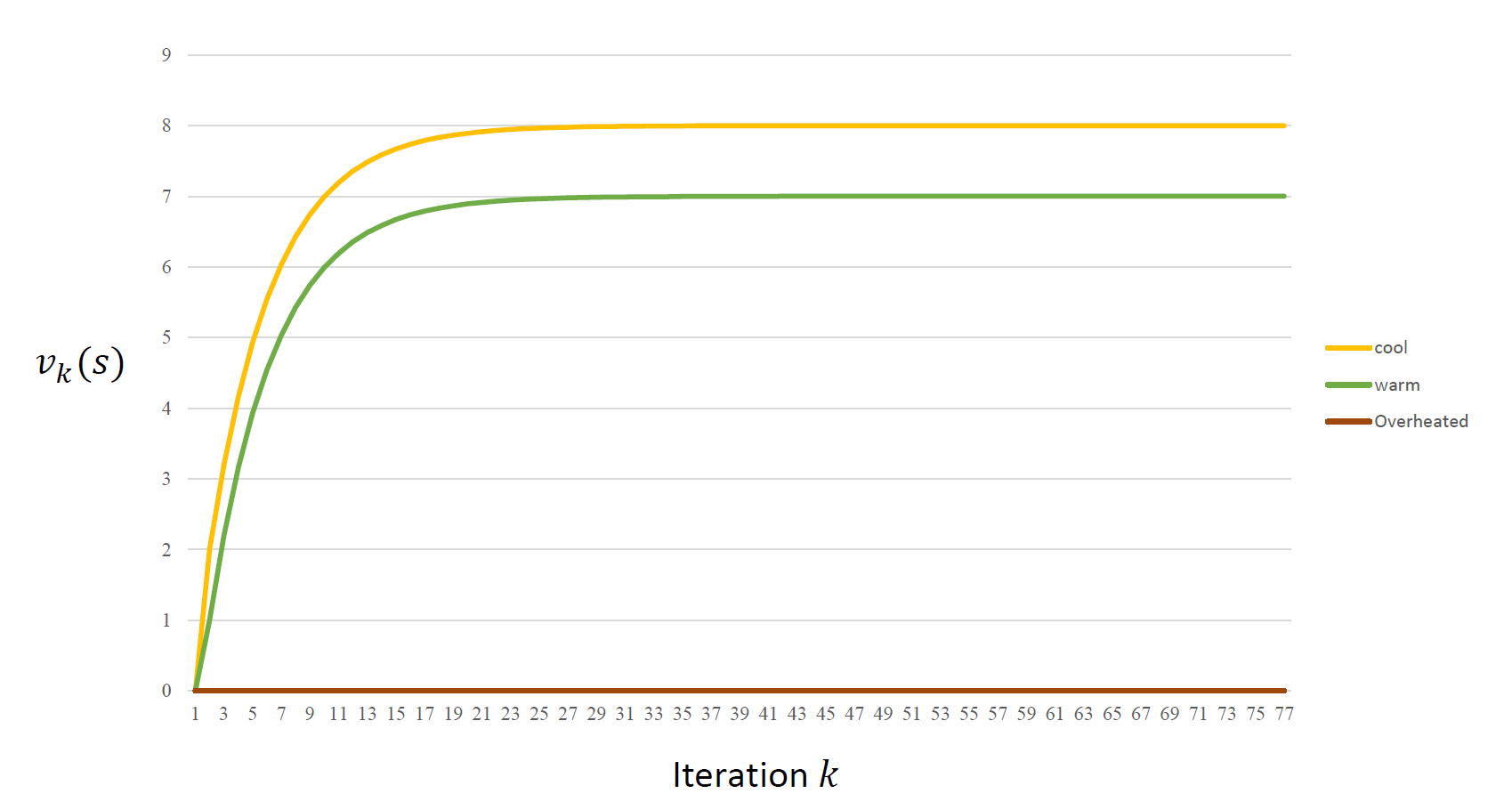
결과
여기서 수렴하는 값은 어떤 상태에서의 누적보상합 기댓값의 최대치를 말하기에 최적 행동 가치 함수를 얻게 된 것
최적 정책
우리가 구하고 싶은 것은 최적 정책이기 때문에 앞에서 최적 가치 함수를 구한 것을 이용해서 어떤 상태 s에 대한 최적 정책을 구해보고자 한다.
이를 통해서 각각의 상태에 대한 최적 정책을 최적 가치함수로 구할 수 있게 된다.
Gambler’s problem
구성요소
- 상태 s: 자산상태로 [1,2,3,4,…]
- 행동 a: 배팅하는 금액으로 [0,1,2,…,min(s, 100-s)]
- 상태전이확률 : 앞면이 나올 확률 = 0.4
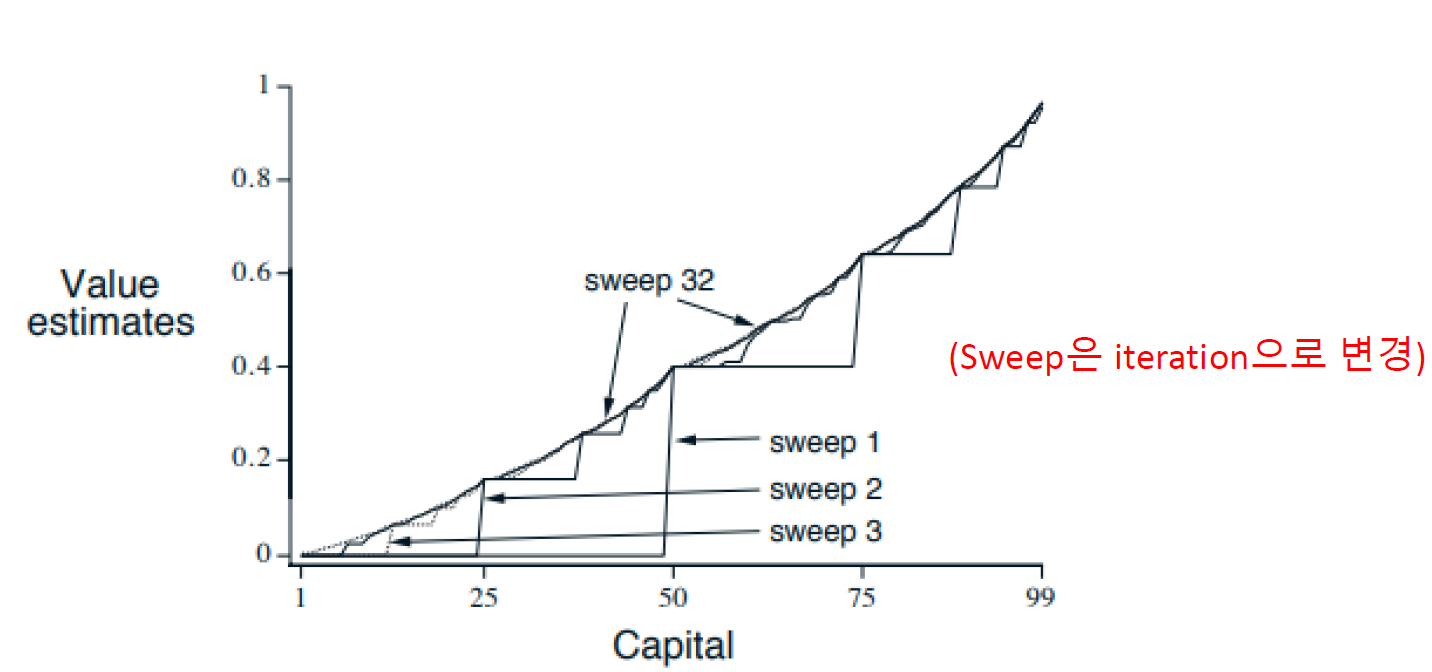
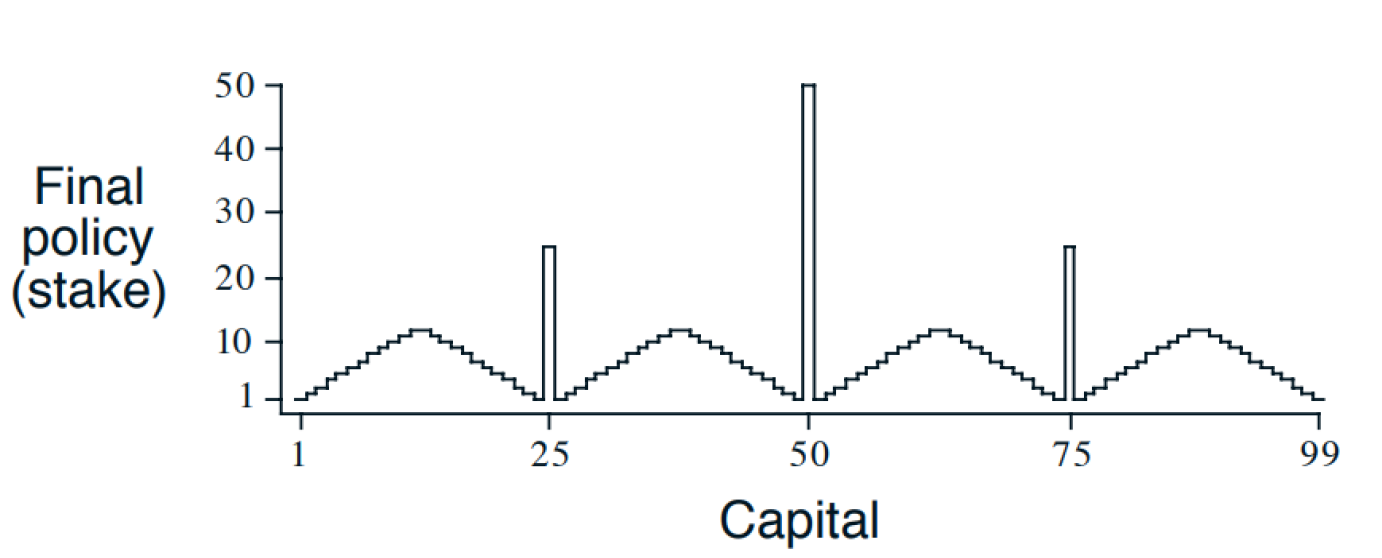
Iteration(Sweep) 결과
이렇게 모든 상태에 대해서 최적 가치함수를 구할 수 있게 된다.
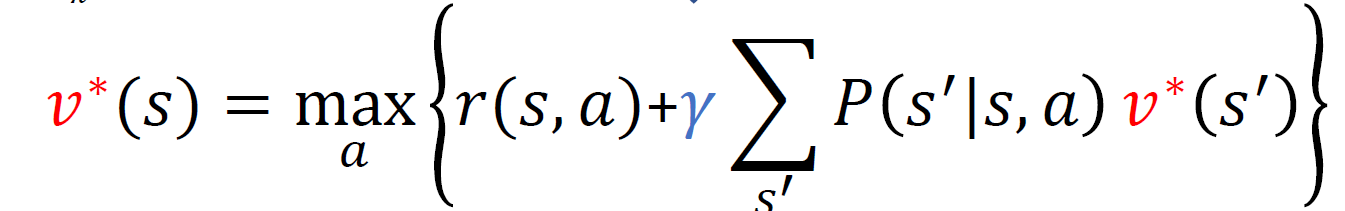


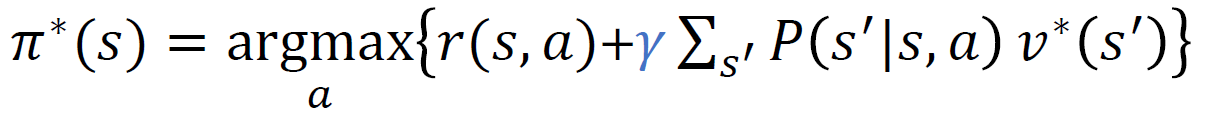
댓글남기기