[KMOOC 강화학습] Week 09-2 Monte Carlo Learning
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
Monte Carlo
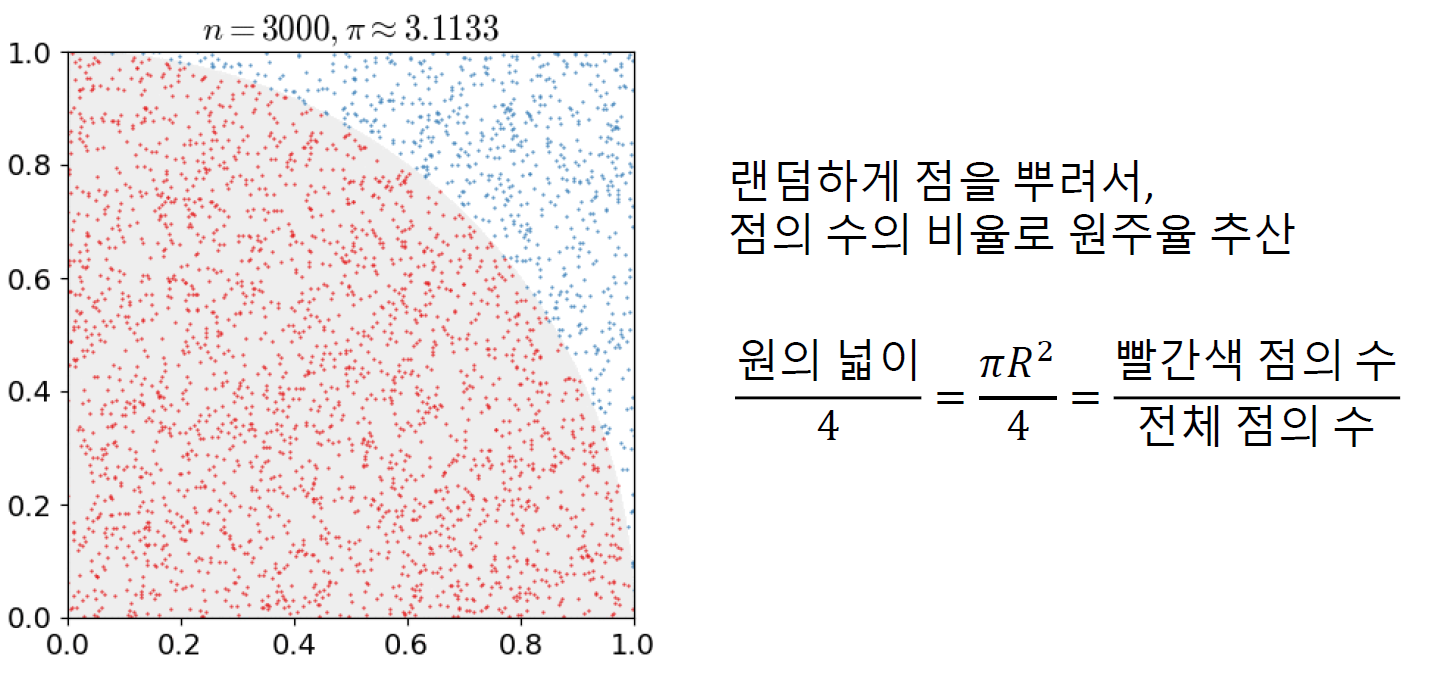
- 장점: 랜덤하게 점을 뿌리고 점의 수의 비율로 추정가능하다
실제 시도로 얻은 데이터로 값을 추정하는 것
즉 에이전트가 환경과 상호작용하면서 얻은 에피소드(상태, 행동, 보상의 나열) 단위로 모은 다음, 가치함수를 추정하게 된다.
에피소드
에피소드는 종료 상태에 오면 끝나는 형태가 되며 에피소드는 독립적이고, 하나의 상태가 한 에피소드에 반복해서 나올 수도 있다.
- 보상 : 현재시점부터 종료까지의 보상들의 합
- 연속 작업: 주가처럼 프로세스가 계속 진행되는 경우를 말한다.
- 누적보상합이 발산할 수 있어서 감가율이 도입된다.
몬테칼로 정책 평가
종결상태이 있는 에피소드를 한정하여 사용한다.
현재 상태에 대해 가치함수 값을 구할 때 무수히 많은 에피소드들에 대해서 구하고 산술평균하게 되면 수렴하게 된다.
First visit MC
최초 방문 시점으로부터 누적보상합을 리턴을 사용하게 되고 동일한 상태가 반복된다면 그것은 상태의 가치함수를 계산할 때 사용하지 않게 된다.
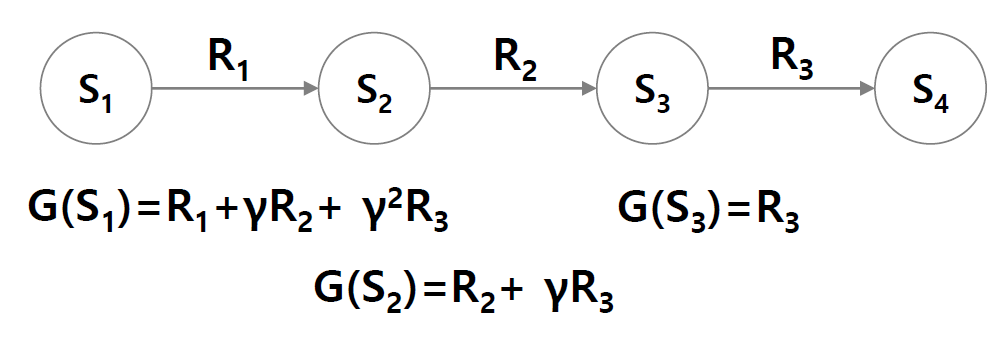
아래의 경우는 상태 3에 대한 리턴을 계산하는 경우이다.
위의 경우에는 상태 3에 도달하는 경우에 2번의 가치함수를 계산할 수 있지만 최초 방문한 것만을 사용한다는 것이다.
Every visit MC
특정 상태에 여러번 방문했다면 모두 다 리턴값을 가지고 오고 가치함수 추정시 사용하게 된다.
이 경우에는 상태 3을 2번 방문하니까 그 때마다 가치함수를 계산하게 되고 이것을 산술평균할 때 사용하게 된다.
점진적 MC 정책평가
100번까지 알고 101번째 에피소드에 대해서 가치함수 추정하고자 할 때
- 101개의 에피소드로 가치함수 추정
- 100개로 추정한 값을 업데이트
기존 가치함수에 차이만큼 업데이트 진행하는 것으로 이렇게 하면 굳이 모든 에피소드에 대한 정보를 다 가질 필요가 없고 최근의 가치함수에 대한 추정치만 가지면 된다.
이 때 새로운 정보에 대한 값에 대한 비중을 learning rate으로 조정하게 된다.
MC 정책 개선
단순히 가치 함수만 계산하는 것이 아니라, 행동-가치 함수 Q(s,a)를 추정하면 특정 상태에서 행동을 선택할 수 있을 것이다.
그 방법으로,
- 특정 상태 특정 행동시 상응하는 리워드가 발생
- 리워드 발생 시점으로부터 리턴값 계산
위의 경우에서 Q(4,->)을 계산해보자
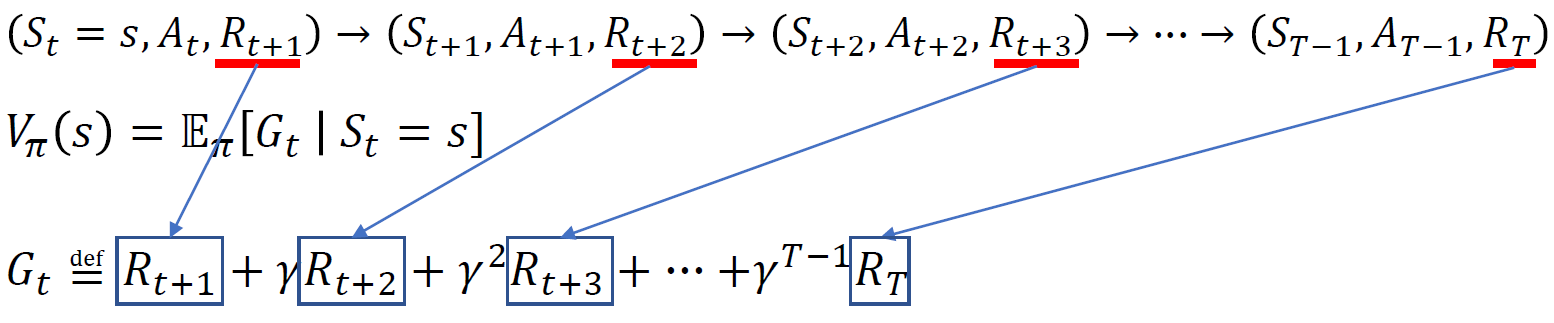

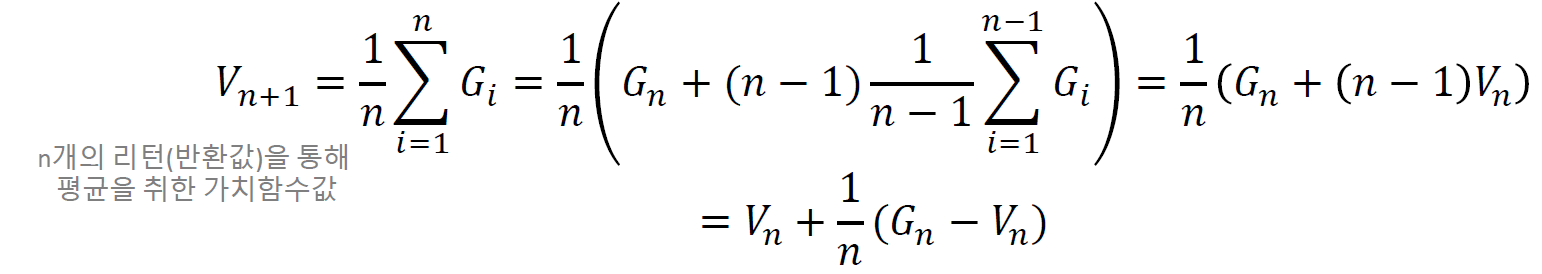

댓글남기기