[KMOOC 강화학습] Week 10-1 Temporal Difference Learning
해당 강의는 K-MOOC의 “강화학습의 수학적 기초와 알고리즘 이해” 수업을 수강하며 기록한 내용입니다. 강의는 링크에서 확인하실 수 있습니다.
개괄
환경에 대한 정보(상태 전이 확률) + 액션에 대한 리워드가 밝혀져있다면, MDP문제로 치환되고 풀 수 있다.
다만 환경에 대한 정보, 보상에 대한 정보가 없는 경우 상호작용으로 풀고자 한다.
그래서 크게 2가지로 구성된다.
- Prediction: 정책에 대한 상태 가치 함수를 계산, 평가하는 과정
- Control: 개선된 정책을 생성하고 최적 정책을 찾아가는 과정
MC
에피소드가 종료될 때까지 진행하고, 모든 상태에 대한 리턴 값을 계산하여 가치함수를 업데이트 하게 된다.
- Prediction: 누적 리워드 합을 계산하는 과정에 해당하며 이 때 방법으로 First Visit과 Every visit, incremental 방식이 있었다.
- Control: 행동가치함수에 대한 추정에 해당하며, 하나의 에피소드를 바탕으로 행동-가치함수를 업데이트 하게 되고 정책을 다시 업데이트 해나가는 방식이다. 이 때 정책을 업데이트 하는 방식은 epsilon greedy 방식을 사용한다.
여기서 epsilon의 역할은, 가장 좋은 행동을 취할 확률이 1-eps가 되는 것. 이렇게 하는 이유는 가장 좋은 행동만 사용하는 것은 exploitation에 해당, 여러 다른 행동들도 보는 경우는 exploration에 해당한다.
즉, 정책이 항상 좋은 best로 가게 되는데 그렇지 않은 경우도 존재한다는 것같다.
문제점
에피소드가 끝날때까지 기다려야 하며 에피소드 샘플이 충분히 많아야 한다.
TD
상태전이 확률, 보상을 모르고, 에피소드가 끝나야 업데이트가 가능했었는데 이 방법은 굳이 에이전트가 종료상태에 도달하지 않더라도 최근에 습득한 정보로 업데이트 하는 방법론이다.
특정 단계에서의 보상은 지금 얻은 데이터로 계산하고 그 이후의 보상은 기존에 학습한 것으로 계산하고, 고려하는 단계를 Step 수로 말하게 되고 1단계만 고려하면 1Step-TD, TD(0)가 된다.
- TD target
- 업데이트 룰
이렇게 계산할 때 수렴하기 위한 조건으로, 업데이트 항(TD-error)이 0이 된다면 수렴했다고 볼 수 있을 것이다!
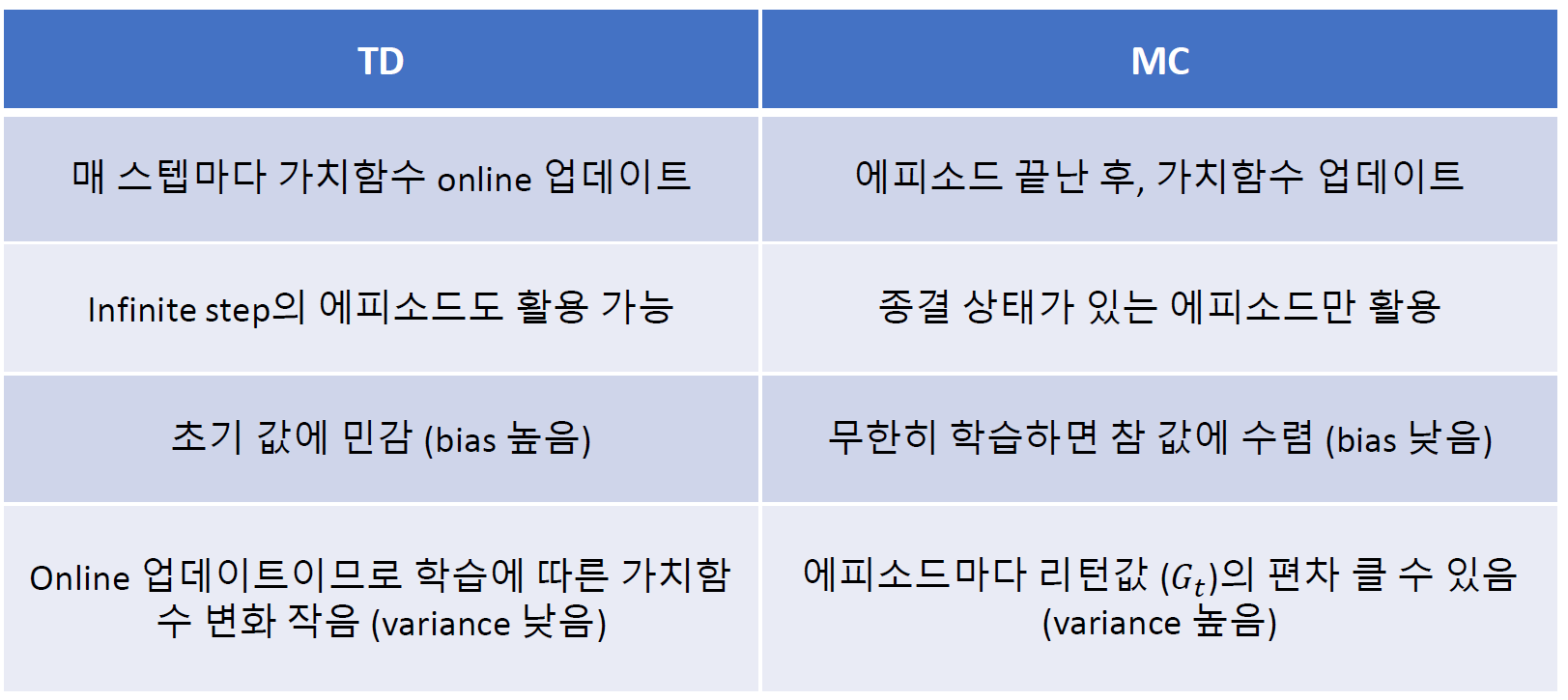
vs MC
이렇게 했을 때 MC는 infinite step TD로 볼 수 있게 된다. 에피소드가 끝날 때까지 고려하게 되니.
- 단계별로 업데이트 하게 된다면 순서에 의한 효과가 있을 것인데 bias가 높다는 것은 결국 순서에 따른 효과로 인해서 생기는 것인가?
정리
MDP는 모든 정보가 있기 때문에 평균적으로 구해놓고 업데이트 하면 된다.
반대로 정보가 없다면 한 에피소드를 다 잡고 계산하는 것이 MC이고 TD는 step 별로 계산하게 된다.

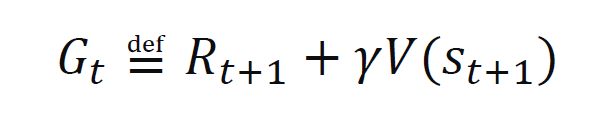
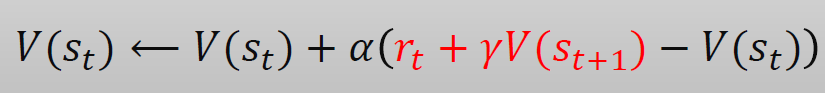
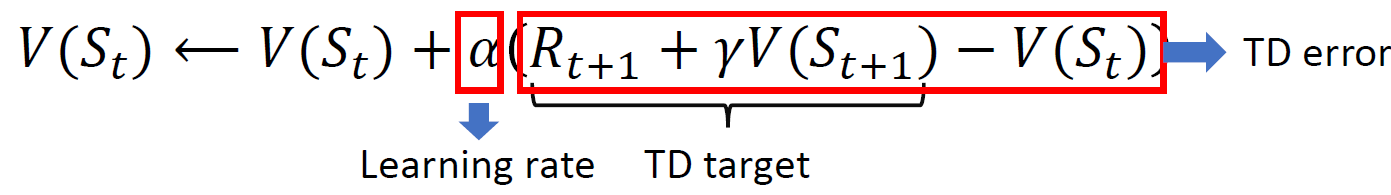
댓글남기기