[Lecture Summary] 06 Algorithm and Data Structure : Binary Tree

This contents is based on Lecture of link

Overview

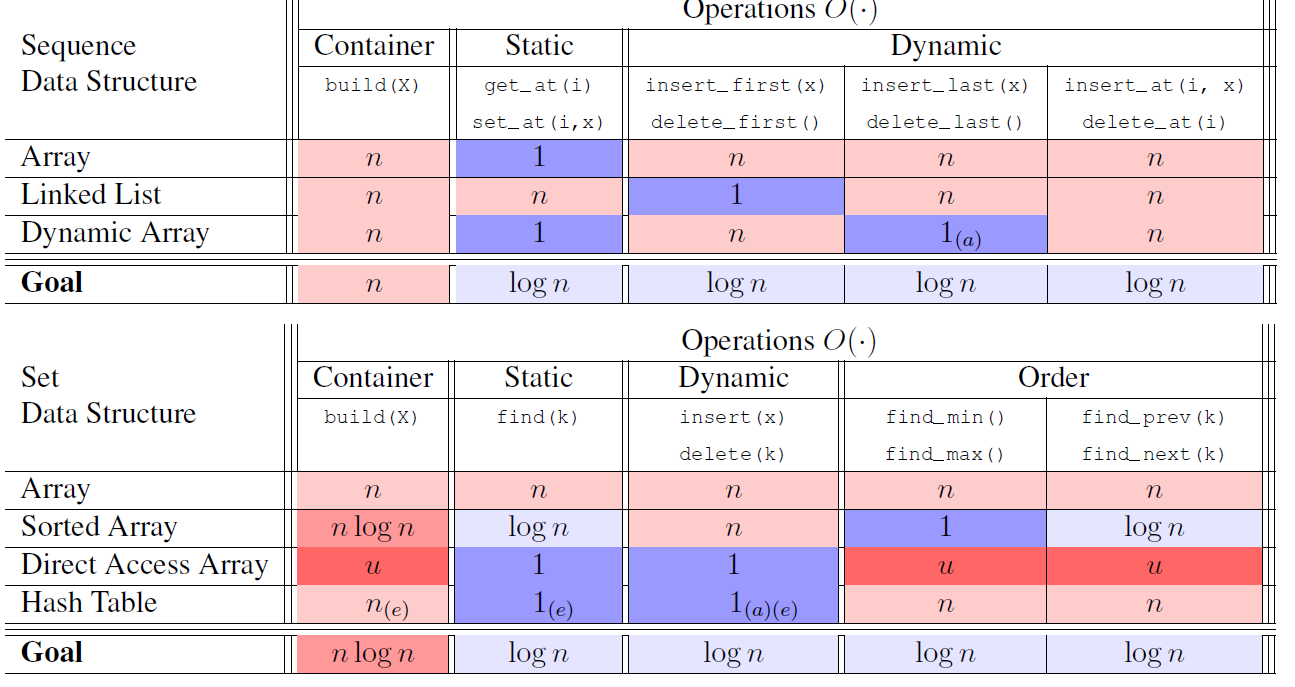
For any kind of Interface, we’d like to acheive efficient, logartihm time scale! This means that any operation on data structure achieve averagely beneficial.

So we suggest binary tree structure.

One thing is that linked list can be considered as a kind of tree structure but its node has only 2 pointers which are pointing previous and next one.
Therefore, depth of linked list is linear which makes opeartion linear time.

However, binary tree is also pointer-based data structure with tree pointers which are parents, left and right pointers.
This can improve into logarithm time scale being depth of $\log(n)$.

Flow

First of all, all the operation takes time proportional to the height of binary tree.
Then prove it that height is logartime time.
Finally, how to assure, or maintain, height is logarithm to the number of nodes(balanced)!

Properties to keep in mind!

Subtree_augmentation

each node can store $O(1)$ extra field or properties

subtree property

anything which can be computed(sum, product, min, max and etc) from properties of node’s children(or node itself, bottom up order!) in $O(1)$ time.
Therefore we can update properties dynamically!

Ex:

• node.size $\gets$ node.left.size + node.right.size + 1
  

• node.height = 1 + max{node.left.height, node.right.height}

• not for index or depth

Terminology

Depth of node $x$

• # of ancestors
• # of edges in path from $x$ up to the root
• (Personally) upward length

Height of node $x$

• # of edges in the longest downward path from $x$
  • all leaves have zero height
• math depth of any node in the subtree rooted at node $x$

Size of node $x$

• # of nodes in subtree($x$) including $x$

Traversal order of binary tree

• It is intrinsic(implicit) order
  • No need to manipulating order array(If you want to make, takes linear time! OOPS!). Tree structure already implies it.
• For node $x$, at the left hand side of it, its predecessor exist and at the right hand side of it, its successor exist.
• Every node in left(right) subtree of node $x$ is before(after) $x$ in this order.
• THEN, we can define in a recursive equation starting from root(top down)

---

Operations

def subtree(node $x$):

• (interface) return subtree rooted at node $x$
  • including node $x$

def subtree_first(node $x$):

• (interface) return node in subtree among subtree($x$) which comes first in a traversal order
• (algorithm)
  • update node $\gets$ node.left util falling off tree(which is node.left = None)
  • return node
• Takes $O(h)$!(because it can reach leaf in the worst case)

def successor/predecessor(node $x$):

• (interface) return next/before node in a traveral order
• (algorithm)
  • if $x$.right/$x$.left exist, return subtree_first($x$.right/$x$.left)
  • else
    • update node $\gets$ node.parrent until x is in left/right subtree
    • return subtree_first(node)
• Takes $O(h)$!(because it can reach leaf in the worst case)

def subtree_insert_after(node $x$, node_new $y$):

• (interace) inters new node $y$ after node $x$
• (algorithm)
  • if x.right does not exist, x.right = y
  • else successor(x).left = y
• Takes $O(h)$!(because it uses successor())

def subtree_delete(node $x$):

• (interface) remove $x$ from its subtree(or traversal order)
• (algorithm)
  • if x is leaf, x.parrent.dirrection = None
  • else if x.left exist(or predecessor($x$) is not None)
    • swap $x$.item & predecessor($x$).item
    • subtree_delete(predecessor($x$))
• Takes $O(h)$ because of function predecessor($\cdot$)

Set Interface: Set Binary Tree, Binary Search Tree(BST)

The thing is that traversal order is same with increasing order of item.key.
This is BST Property which is satisfying following relation

• every key in left subtree $\le$ node’s key $\le$ every key in right subtree.

THEN, finding operation is binary search which takes $O(h)$!.

Operation for Set Interface

Operation to support is insert/delete. This changed the structure of some “part”. Then which structure has been changed after these operations?

• Updates on only ancestors in order up the tree.
• More specifically, subtrees whose ancestors act as a root node
  • you can think of an induction that single change of node can affect the ancestors.
  • On the other hand, there must exist subtrees which do not change after operations.

def subtree_find(node $x$, key $k$):

• if $x$ is None, return None
• if $k < x$.item.key, recurse on $x$.left
  • $x\gets x$.left, subtree_find($x$, $k$)
• if $k = x$.item.key, return $x$
• if $k > x$.item.key, recurse on $x$.right
  • $x\gets x$.right, subtree_find($x$, $k$)

Time analysis

• all the operations take logarithm time
• takes $O(n\log(n))$ for build
• takes $O(n)$ for iteration

Sequence Interface: Sequence Binary Tree

traversal order is same with sequence order

def subtree_at(node $x$, index $i$):

• $n_L$ = size($x$.left)
• if $i< n_L$, then subtree_at($x$.left, $i$)
• if $i= n_L$, then return $x$
• if $i> n_L$, then subtree_at($x$.right, $i-n_L-1$)
  • $i-n_L-1$ : make starting index as zero! starting index points at starting node of traversal order

Time analysis

• all the operations take logarithm time
• takes $O(n)$ for build and iteration

Height Balance

To support dynamic operations, use “Balanced” B-Tree! Balanced means that binary tree maintains logarithm time under dynamic operations.

To make height balance, we need to assure following statement

• height(node.left) - height(node.right) $\in$ {-1,0,1}
• This implies $h=O(\log(n))$

There are many schema to make balance. Strcuture will be changed while internal semantics like traversal order is reserved. And the way to do so is Rotation. This requires every node in tree to be changed and, as a result, takes $O(n)$ just like updating depth. So, we need to use ANOTHER WAY to acquire $\log(n)$ time! The first schema was the AVL Tree.

AVL Trees

For tree structure we can have following equation

• $N_h$ : height of node $N$ = h
• $N_{h-2}$ : height of one subtree = h-2
• $N_{h-1}$ : height of the other subtree = h -1
• Height balance : $N_h = N_{h-2} + N_{h-1} + 1$
  • skew is the difference between heights of subtrees
• $N_h \ge 2 N_{h-2}$
• $N_h \ge 2^{[h/2]}$ : geometric series!
• $h \le 2\log(n)$

Now then we can say that height is logarithmic to the number of nodes.

How to update?

Update rules come from the constraint on skew. It should be less than 2. We can think of case for skew $\in$ {-2, 2}. All the node in subtree is height-balanced.

To obtain balance, we can rotation in a specific way. We can devide cases with respect to it children.

• Case 1: skew of children’s height is 1
• Case 2: skew of children’s height is 0
• Case 3: skew of children’s height is -1

We can repeated update tree structure via rotation in a way to reduce bigger subtree! And any modification on tree structure can be considered as one of the above cases. Then we can adjust tree structure with logarithm time scale!