[Lecture Summary] 12 Algorithm and Data Structure : Single Source Shortest Path

This contents is based on Lecture of link

Overview

We do not cover undirected graph because negative edge makes negative weight cycle!

DAG Relaxation

Beause our interest of graph is DAG, we can compute topological order with finishing order of G.

• Idea

Maintain a distance estimate $d(s,v)$ which is initialized as infinitiy for every vertex. We can think of this strategy as gradually lowering the upper bound by updating distance estimates.

=> start from overestimates and lower it!

• Triangle inequality

the shortest path weight from $u$ to $v$ cannot be greater than the shortest path from $u$ to $v$ through another vertex

$\delta(u,v) \le \delta(u,x) + \delta(x,v)$ for all $u,v,x \in V$

• Update condition

Update when triangle inequality does not satisfy. The thing is that estimates are not correct so we define update condition as follows:

$If (u,v) \in E s.t. d(s,v) > d(s,u)+w(u,v)$ then $d(s,v) \gets d(s,u) + w(u,v)$
In this case, we say that we relax $(u,v)$ which make shortest path from $s\to v$ to $s\to u \to v$

• Safe relaxation

When maintaing each distance estimates $d(s,v)$ is a $w(\pi)$ from $s$ to $v$!

(Proof) In the algorithm we update distance as cumulative summation of weight!

Algorithm

• Initialize $d(s,v) = \infty $ for all $v \in V$
• Set $d(s,s) = 0$
• $u \in V$ along with the topological order of G(G is DAG!!)
  • For each $v \in Adj^+(u)$
    • If update condition is satisfied, relax edge!

Runtime

Task	Time
Initialzie	$O(\mid V \mid)$
Topological order sorting	$O(\mid V \mid + \mid E \mid)$
Iterating $Adj^+$	$O(1)\times \sum_{u\in V} deg^{+}(u) = O(\mid E \mid)$

Bellman-Ford

This algorithm is devised to

• solve weighted shortest path with cycle & negative weights.
• return for all vertices
  • unreachable vetex returns infinity
  • reachable via negative cycle return negative infinity
• $k$-Edge Distance

$\delta_k(s,v)$ weight of a shortest path from $s$ to $v$ using less than $k$ edges!

Negative Cycle Witness

• THe first statement!

If $\delta(s,v) \ne - \infty$, $\delta(s,v) = \delta_{\mid V \mid -1}(s,v)$ since a shortest path is simple!

If $\delta_{\mid V \mid} (s,v) < \delta_{\mid V \mid -1}(s,v)$ then there exist a shorter non-simple path which implies $\delta_{\mid V \mid}(s,v) = - \infty$ and negative cycle.

Then we say that it is a witness vertex $v s.t.$ belongs to negative cycle.
That’s why it is shorter distance with more vertices!

The thing is that inverse statement does not hold! There could be exit a vertex with $\delta = -\infty$ but does not satisfies that inequality.

• The second statement!

If $\delta(s,v) = -\infty$ then $v$ is reachable from a witness

Every negative weight cycle is reachable from witniess! We can prove it with triangle inequality.

• Summary

1. If K-edge distance constraint does not hold, it is a witness
2. If a vertex is witness then it is reachable from that vertex

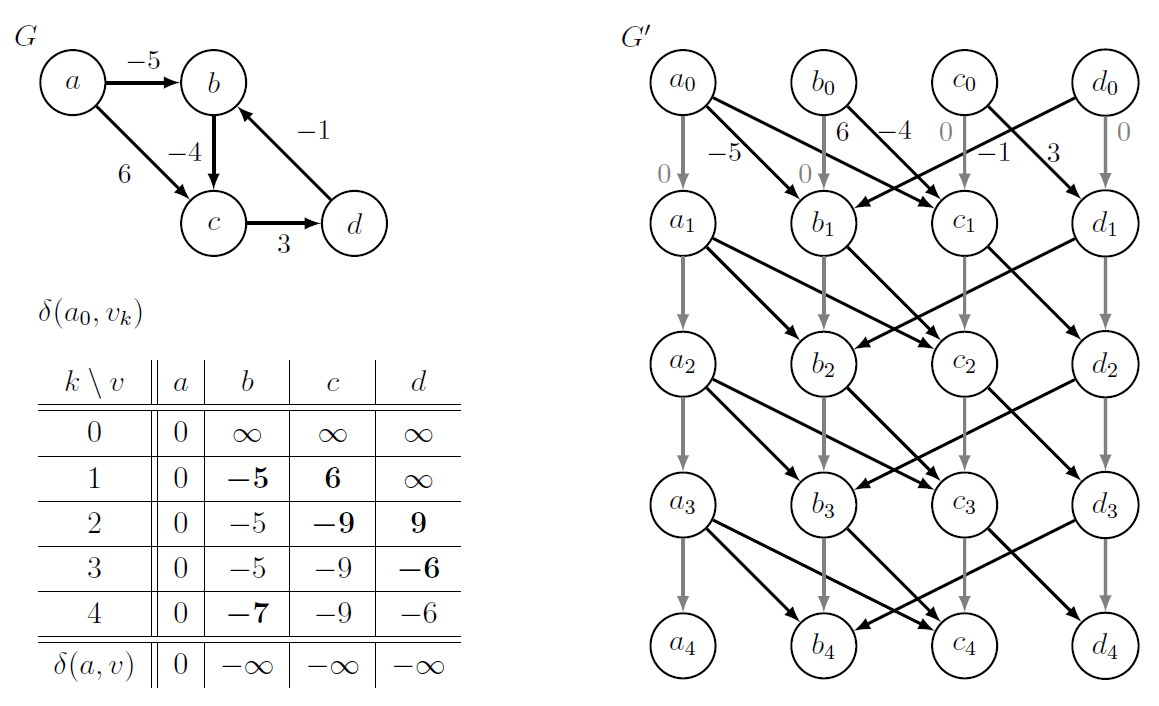
Graph Duplication

make $\mid V \mid +1$ levels of duplicates!

According to the above figure, it is a DAG and we can run DAG relaxation so that we can compute distances from $s_0$ to every vertex at level $k$.

Algorithm

• Run graph duplication and return new graph G’
• Run DAG Relxation on G’ from $s_0$ and compute all distances from $s_0$
• For each vertex, $d(s,v) \gets \delta(s_0, v_{\mid V \mid -1})$
• For each witness $u \in V$
  • For each vertex $v$ reachable from $u$, set $d(s,v) = - \infty$

Correctness

We need to prove that

• k-edge distance between $s$ and $v$ is equal to distance between $s_0$ and $v_k$
• estimates converges to real distances!

Run time

Process	Time
Construction	$O(\mid V \mid (\mid V\mid + \mid E\mid)) $
DAG Relaxation	linear
Witness $\times$ reachable	$O(\mid V\mid \mid E\mid)$

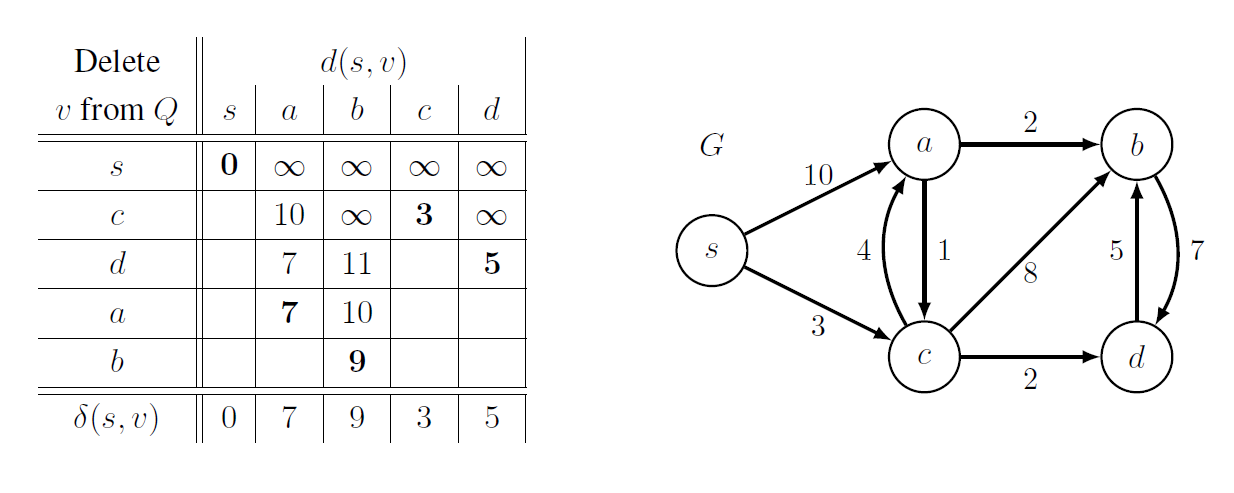
Dijkstra’s Algorithm

This algorithm is devised to solve weighted shortest path of general graphs with non-negative weights. We can comprehend it as a generalization of BFS.

Before we start, let’s think of a kind of a sphere centered at source $s$. From the center, we’d like to find closer vertices so that we can gradually compute distances!

• That’s why we constrain on non-negative weight edges(monotonic increasing distances!)
• weakly monotonic increasing for zero-weighted edges

Moreover, we can solve SSSP in a faster way if we sort vertices in increasing distance order.

Data Structure

According to the above insights, we need to devise a new data structure so that we can relax edges from each vertex in increasing order of distance.
For Changable Priority Queue, its IDs is sorted so that we can delete item with minimum key.

To implement it, we can simply use regular priority queue $Q’$ and dictionary which maps ID into $Q’$.
✔️ We can replace dictionary with hash table or DAA to acquire constant time. ✔️ distance as a key and integer based id as a id(or label)

Algorithm

• Set every distance as infinity except source node itself.
• For nodes which do not satisfy triangle inequality, relax edge and decrease the key(or distance estimates)

Correctness

• Convergence: Algorithm sets initial distance values as an infinity and decrease it! Once estimates becomes true value, the algorithm naturally stops.
• Assurance whether Estimates = True value : Use Induction!

Runtime

Operation	Time	Occurrence in Algo
build(x)	$B_n$	1
delete_min()	$M_n$	$\mid V\mid$
decrease_key(id, k)	$D_n$	$\mid E\mid$

Total Learning Time is $O(B_{\mid V\mid}+\mid V\mid \cdot M_{\mid V\mid}+\mid E\mid \cdot D_{\mid V\mid})$

As you can look at the above feagure, we can choose data structure according to whether graph is dense or not.